Trigonometria
A Trigonometria é um ramo da matemática que estuda as relações entre os lados e os ângulos de um triângulo. Ela é essencial para entender fenômenos periódicos, construir pontes, calcular distâncias e até mesmo para criar gráficos em jogos digitais
Triângulo Retângulo
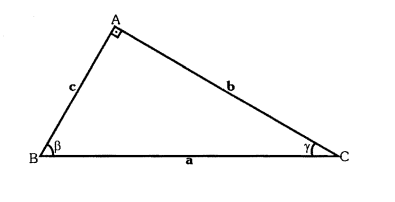
O triângulo ABC é retângulo em A, pois forma ângulo de 90°
Temos:
- a é a hipotenusa (sempre vai ser o lado oposto ao ângulo reto (A)
- Em relação ao ângulo [math] \beta [/math], b o cateto oposto e c é o cateto adjacente
- Em relação ao ângulo [math] \gamma [/math], b o cateto adjacente e c é o cateto oposto
- [math] \beta [/math] e [math] \gamma [/math] são ângulos complementares isto é:
[math]\beta+\gamma= 90°[/math]
Teorema de Pitágoras
“O quadrado da hipotenusa é igual à soma dos quadrados dos catetos.”
Demonstrando a afirmação acima em equação, temos:
[math]a^{2}=b^{2}+c^{2}[/math]
Exercício
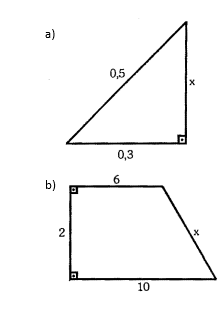
Calcule o X em cada caso:
Solução
a) [math]0,5^{2}=0,3^{2}+x^{2}[/math]
[math]x=\sqrt{0,25-0,09}[/math]
[math]x=0,4[/math]
b)
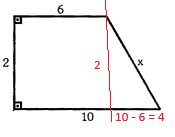
[math]x^{2}=2^{2}+4^{2}[/math]
[math]x=\sqrt{4+16}[/math]
[math]x\cong 4,47[/math]
Razões trigonométricas
As razões trigonométricas são ferramentas que nos ajudam a relacionar os lados de um triângulo retângulo com seus ângulos.
Assim, considerando o triângulo retângulo ABC da figura, temos as seguintes conclusões:
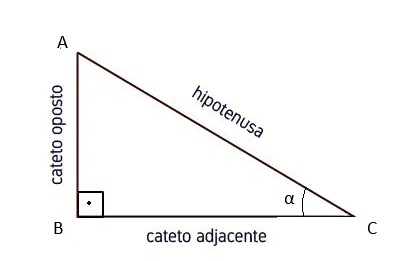
- O seno de um ângulo agudo mede o cateto oposto em relação à hipotenusa.
[math]\sin\alpha = \frac{\text{cateto oposto}}{hipotenusa}[/math]
- O cosseno de um ângulo agudo mede a cateto adjacente em relação à hipotenusa.
[math]\cos\alpha = \frac{\text{cateto adjacente}}{hipotenusa}[/math]
- Tangente de um ângulo agudo mede o cateto oposto em relação ao cateto adjacente
[math]\tan\alpha = \frac{\text{cateto oposto}}{\text{cateto adjacente}}[/math]
Uma dica para memorizar as razões é a palavra SOHCATOA
- S é o seno, C é o cosseno e T é a tangente
- O, é o cateto oposto, A é o cateto adjacente e H é a hipotenusa
Dado esses conceitos, três ângulos são muito usados em cálculos trigonométricos, esses ângulos são chamados de ângulos notáveis, que são 30°, 45° e 60°. A tabela dos ângulos notáveis é um dos recursos mais úteis na trigonometria.
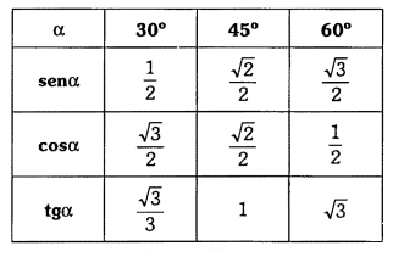
Um macete para memorizar a tabela cante a letra a seguir ao ritmo da música “Bate o sino”:
“1, 2, 3
3, 2, 1
Tudo sobre 2
A raiz vai no 3 e também no 2
A tangente é diferente, vejam só vocês
Raiz de 3 sobre 3, 1, raiz de 3″
Segue um exemplo pra ajudar!
(UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) 2√3
b) √3/3
c) √3/6
d) √20/20
e) 3√3
Solução
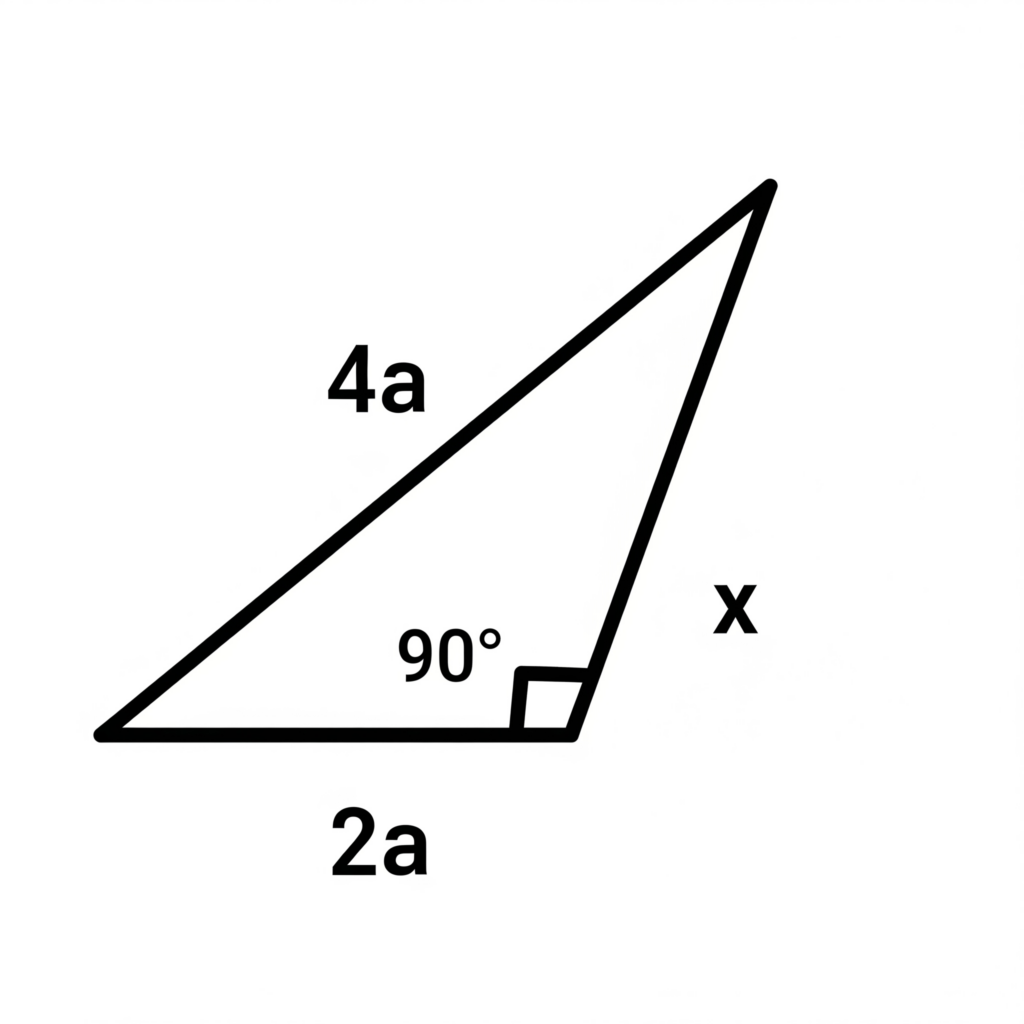
Primeiro precisamos descobrir o menor lado, então vamos calcular o valor de X:
[math](4a)^{2}=(2a)^{2}+x^{2}[/math]
[math]16a^{2}=4a^{2}+x^{2}[/math]
[math]16a^{2}-4a^{2}=x^{2}[/math]
[math]x^{2}=12a^{2}[/math]
[math]x=\sqrt{12a^{2}}[/math]
[math]x=2a\sqrt{3}[/math]
Agora conseguimos ver que o menor lado é o 2a, então vamos fazer a tangente do ângulo oposto ao menor lado:
[math]\tan\alpha=\frac{2a}{2a\sqrt{3}}[/math]
[math]\tan\alpha=\frac{1}{\sqrt{3}}[/math]
[math]\tan\alpha=\frac{1}{\sqrt{3}}*\frac{\sqrt{3}}{\sqrt{3}}[/math]
[math]\tan\alpha=\frac{\sqrt{3}}{3}[/math]
Resposta: b
Exercícios
01. (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
A) 6√3 m.
B)12 m.
C)13,6 m.
D) 9√3 m.
E)18 m.
02. (UFJF) A uma tela de computador está associado um sistema de coordenadas cartesianas, com origem no canto inferior esquerdo. Um certo programa gráfico pode ser usado para desenhar na tela somente retas de inclinações iguais a 0°, 30°, 45°, 60° e 90° em relação ao eixo horizontal. Então, considerando-se os pontos a seguir, o único que não pode estar sobre uma reta, a partir da origem, desenhada por este programa é:
A)(0, 10√3)
B)(10√3)
C)(10√3, 10√3)
D)(10√3, 5√3) x
E)(10√3, 5)
03. (UECE) Seja AEC um triângulo isósceles (as medidas dos lados AE e AC são iguais) e O um ponto do lado AC tal que a medida do ângulo EÔC é 120 graus. Se existe um ponto B, do lado AE, tal que o segmento OB é perpendicular ao lado AE e a medida do ângulo EÔB seja igual a 40 graus, então a medida do ângulo OÊC, em graus, é igual a
A) 9
B)7
C)5
D) 3
04. (Unicamp) Ao decolar, um avião deixa o solo com um ângulo constante de 15º. A 3,8 km da cabeceira da pista existe um morro íngreme. A figura abaixo ilustra a decolagem, fora de escala. Podemos concluir que o avião ultrapassa o morro a uma altura, a partir da sua base, de
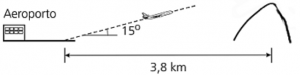
A) 3,8 tan (15°) km.
B) 3,8 sen (15°) km.
C) 3,8 cos (15°) km.
D) 3,8 sec (15°) km.
05. (Fuvest) Dentre os números a seguir, o mais próximo de sen50° é:
A) 0,2
B)0,4
C)0,6
D) 0,8
06. (Ufsm) Um estudante de Engenharia vê um prédio do Campus da UFSM construído em um terreno plano, sob um ângulo de 30°. Aproximando-se do prédio mais 40m, passa a vê-lo sob um ângulo de 60°. Considerando que a base do prédio está no mesmo nível do olho do estudante, então a altura h do prédio é igual a
A) 30Ë3 m.
B) 20Ë3 m.
C) 30 m.
D) 10Ë3 m.
E) 28 m
1. E
2. D
3. C
4. A
5. D
6. B
