Matemática Financeira
A Matemática Financeira é um campo da matemática aplicada que estuda as relações entre o valor do dinheiro ao longo do tempo, considerando conceitos como juros, descontos, amortização, financiamentos, investimentos e inflação. Ela se baseia em uma série de técnicas e cálculos matemáticos que permitem analisar operações financeiras e tomar decisões fundamentadas em cenários de incerteza, como nos mercados de crédito e de investimentos.
O principal objetivo da Matemática Financeira é fornecer as ferramentas para resolver problemas que envolvem o fluxo de dinheiro no tempo, como o cálculo de juros, o financiamento de bens, o valor de um investimento e a comparação entre diferentes alternativas financeiras. É fundamental tanto para indivíduos quanto para empresas, pois permite a análise e o planejamento financeiro.
Juros – Definição
Podemos definir juros como o valor de um aluguel para o dinheiro, ou seja, a remuneração que o credor (pessoa que empresta o dinheiro) receberá pelo tempo que ficará sem utilizar o seu próprio recurso.
Vamos exemplificar para ficar mais fácil…
Vamos supor que João quer muito comprar um computador de R$ 1.000 que entrou em uma promoção muito boa que irá durar apenas um dia, mas ele não possui dinheiro naquele momento, porém seu melhor amigo Marcio tem um dinheiro guardado que não irá usar no momento e decide emprestá-lo para o João cobrando 10% de juros por mês. Esse valor de 10% cobrado por Marcio é como se fosse uma remuneração que ele receberia pelo tempo que ele ficou sem o seu dinheiro, e é essa a definição de juros que precisamos ter em mente.
Elementos de uma operação com Juros
Antes de iniciarmos, vamos conhecer os termos usados dentro de uma operação com Juros.
- Capital (C): Valor inicial, pode ser o valor que pegou emprestado ou também o valor investido
- Juros (J) vs. Taxa de Juros (i): Juros é o valor que deverá ser pago a mais em caso de um empréstimo ou então ou valor que irá receber em um investimento, enquanto a taxa de juros (i) é o percentual, o coeficiente que irá definir o valor do capital em uma unidade de tempo (pode ser por mês, por dia, por ano, etc..)
- Tempo (t): Para a matemática financeira, temos que o tempo é o número de períodos em que irá ocorrer a operação, o período que o devedor fica com o empréstimo ou o período que o valor fica investido.
- Montante (M): É o valor final já considerando os juros, portanto podemos considerar que o montante é o valor do Capital somado ao valor dos juros no período determinado.
Agora que já sabemos as definições teóricas para a matemática financeira, vamos falar um pouco sobre como os modos que os juros podem ser aplicados em um capital, iniciando com as definições de Juros Simples e Juros Compostos.
Juros Simples
No método de Juros Simples os juros são sempre iguais em todos os períodos e ele SEMPRE será aplicado sobre o Capital inicial. Vamos ver um exemplo prático?
Considerando que você pegou R$ 1.000 emprestado com o combinado de pagar 10% ao mês com o método de Juros Simples.
| Período (mês) | Juros (J) | Montante (M) |
| 1 | J = 1.000 * 0,1 = 100 | R$ 1.100 |
| 2 | J = 1.000 * 0,1 = 100 | R$ 1.200 |
| 3 | J = 1.000 * 0,1 = 100 | R$ 1.300 |
| 4 | J = 1.000 * 0,1 = 100 | R$ 1.400 |
Nota-se que o cálculo dos juros foi sempre feito com base no valor de R$ 1.000, portanto ficando sempre com o valor de R$ 10. Portanto, o valor do Montante (M) cresce de uma maneira linear conforme vai avançando a quantidade de períodos.
Juros Compostos
Nos Juros Composto, diferente dos Juros Simples, a taxa de juros é calculada sempre sobre o Montante (M) anterior, ou seja, sobre o Capital somado aos juros aplicados no período anterior. Vamos usar os mesmo valores usados para exemplificar os juros simples, só que agora com o método de Juros Compostos.
| Período (mês) | Juros (J) | Montante (M) |
| 1 | J = 1.000 * 0,1 = 100 | R$1.100 |
| 2 | J = 1.100 * 0,1 = 110 | R$ 1.210 |
| 3 | J = 1.210 * 0,1 = 121 | R$ 1.331 |
| 4 | J = 1.331 * 0,1 = 133,1 | R$ 1.464,1 |
Nota-se que nesse caso, conforme é avançado o período o valor dos juros é alterado, diferentemente do método de juros simples em que o valor dos juros é sempre o mesmo. Isso se dá pois no método de juros compostos para calcular os juros do período é necessário incorporar os juros do período anterior. Com base nisso, podemos notar que o Montante (M) nesse caso cresce de uma maneira exponencial.
Desconto Simples
O desconto simples é uma forma de desconto em que a redução do valor futuro (valor nominal) é calculada de maneira linear, ou seja, o desconto é calculado sobre o valor inicial da operação e permanece constante ao longo do período.
A fórmula utilizada para calcular o desconto simples é:
D=P⋅i⋅t
D = Desconto
PPP = Valor nominal (valor a ser pago no futuro)
iii = Taxa de desconto por período
ttt = Tempo (número de períodos)
Vamos supor que uma empresa tenha um pagamento de R$ 10.000 a ser realizado daqui a 6 meses, e a taxa de desconto simples seja de 10% ao ano (ou 5% por semestre). O desconto seria calculado da seguinte forma:
D=10.000⋅0,05⋅1=500
O valor presente (o valor que a empresa pagaria imediatamente) seria:
VP=10.000−500=9.500
Portanto, a empresa poderia pagar R$ 9.500 agora para quitar sua dívida de R$ 10.000, que venceria daqui a 6 meses.
Desconto Compostos
O desconto composto leva em consideração a capitalização composta, ou seja, o efeito de juros que se acumulam ao longo do tempo. O cálculo do desconto composto é mais complexo, pois o desconto é calculado de forma exponencial, considerando a taxa de desconto e o número de períodos.
A fórmula para o cálculo do desconto composto é:
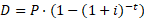
D = Desconto composto
PPP = Valor nominal (valor a ser pago no futuro)
iii = Taxa de desconto por período
ttt = Número de períodos
Agora, vamos calcular o desconto composto. Suponha que você tenha uma dívida de R$ 10.000 a ser paga em 6 meses, e a taxa de desconto composta seja de 10% ao ano (ou 5% por semestre). O desconto seria calculado da seguinte forma:
D=10.000⋅(1−(1+0,05)−1)
Primeiro, calculemos (1+0,05)−1:
Agora, substituímos na fórmula do desconto composto: D=10.000⋅(1−0,9524)=10.000⋅0,0476=476D = 10.000 \cdot (1 – 0,9524) = 10.000 \cdot 0,0476 = 476D=10.000⋅(1−0,9524)=10.000⋅0,0476=476
O valor presente seria: VP=10.000−476=9.524VP = 10.000 – 476 = 9.524VP=10.000−476=9.524
Portanto, o valor presente que seria pago agora, considerando o desconto composto, seria de R$ 9.524.
