Áreas Geométricas

Na geometria o conceito de área plana é a medida da superfície ocupada por uma figura em um plano, nos mostrando o “espaço” que uma figura ocupa. Ela pode ser expressa em unidades de medidas diferentes, como: centímetros quadrados (cm²), metros quadrados (m²), quilômetros quadrados (km²), dentre diversas outras unidades.

Para calcular a área de uma figura plana, usamos uma fórmula que varia de acordo com o formato de cada figura, sendo as principais: o triângulo, o círculo, o quadrado, o retângulo e o trapézio. Mas, geralmente, para encontrar a área de uma figura basta multiplicar a base (b) pela altura (h).

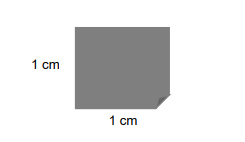
Podemos utilizar como exemplo uma folha de papel quadrada de 1 cm por 1 cm, esta folha ocupa exatamente 1 cm², como mostrado na figura abaixo.

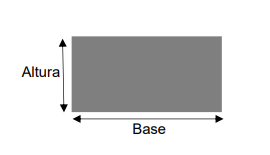
• Área do Retângulo

O retângulo tem lados opostos iguais, então ao multiplicar a base (um dos lados) pela altura (lado perpendicular à base), obtemos quantas unidades quadradas preenchem a figura.\[
Área = Base \cdot Altura
\]

Vamos pegar como o exemplo um retângulo que possui a base de 5 cm e altura de 3 cm, então temos: \[
Área = 5 \cdot 3 = 15 \, \text{cm}^2
\]

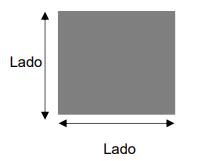
• Área do Quadrado

Como o quadrado tem todos os lados iguais, a área é simplesmente o lado multiplicado por ele mesmo: \[
Área = Lado^2
\]

Para exemplo de cálculo podemos pegar um quadrado com lado de 2cm, então temos: \[
Área = 2^2 = 4 \, \text{cm}^2
\]

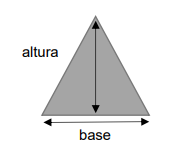
• Área do Triângulo

A área do triângulo é a medida da sua superfície, podendo ser calculada multiplicando a sua base pela altura e dividindo por dois, considerando qualquer triângulo. \[
Área = \frac{Base \cdot Altura}{2}
\]

Um exemplo é um triangulo com base de 2cm e altura de 5 cm, então calculamos da seguinte forma: \[
Área = \frac{2 \cdot 5}{2} = 5 \, \text{cm}^2
\]

• Área do Trapézio

O trapézio tem duas bases de tamanhos diferentes, e por isso, calculamos uma média dessas bases ao somá-las e dividir por 2.

\[
Área = \frac{(Base Maior + Base Menor) \cdot Altura}{2}
\]

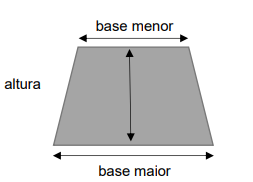
Um exemplo, um trapézio com base maior de 12 cm, base menor de 8 cm, e altura de 4 cm. \[
Área = \frac{12 + 8}{2} \cdot 4 = 40 \text{cm}^2
\]

• Área do Círculo

A área do círculo é obtida multiplicando o valor de π pelo quadrado do raio, normalmente usamos π ≈ 3,14. Lembrando que o raio é a medida do centro da circunferência até sua extremidade, como mostrado na figura a baixo. 

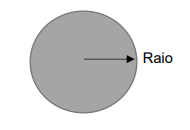
Exemplo de uma circunferência de raio de 4 cm, calculamos da seguinte maneira:\[
Área = \pi \cdot 4^2 = \pi \cdot 16 \approx 50,24 \text{cm}^2
\]

Em resumo, aprender sobre áreas de figuras planas é essencial na geometria, pois nos ajuda a medir o espaço que cada forma ocupa no plano. Cada figura tem uma fórmula própria para calcular a área, usada de acordo com suas características, como a base e altura de um triângulo ou o raio de um círculo. Entender essas fórmulas facilita resolver problemas do dia a dia, como organizar espaços e calcular materiais, destacando a importância da geometria em nossas vidas.

Exercicio de aplicação 

No projeto de uma casa temos o desenho de uma área de lazer no formato de um quadrado, com 8 metros de lado. Nessa área de lazer haverá uma piscina circular com 2 metros de raio, e a área restante será utilizada para a construção do restante da área de lazer (churrasqueira, balcão, cadeiras, mesa, pia, dentre outros.). Nessas condições, a área do espaço de confraternização medirá quanto ? (Use π = 3,14)

Resposta: inicialmente sabemos que o calculo da área de confraternização nada mais é que a diferença entre a área do quadrado de lado medindo 8 metros e a área do círculo de raio medindo 2 metros. Então assim, calculamos as respectivas áreas:

• Área do quadrado ( área de lazer) \[
  Área = 8^8 = 64 \, \text{m}^2
  \]
• Área circulo (área piscina)\[
  Área = \pi \cdot 2^2 = \pi \cdot \approx 12,56 \text{cm}^2
  \]
• Finalmente calculamos a area de confraternização\[
  Área = 64-12,56 = 51,44 \, \text{m}^2
  \]