Estatística Básica
Contextualizando:

Agora que entendemos que estatística está em tudo, é inevitável não estudar esse conteúdo.
Conceitos Teóricos
| Média | Mediana | Moda |
|
É um valor que representa um “equilíbrio” de dados, obtido pela soma de todos os termos e dividido pela quantidade de termos.
Exemplo:
11+12+13+11+16+19+15+18+14=129
129÷9 ≅ 14 A média é, aproximadamente 14.
|
É o valor que fica exatamente no meio do conjunto.
Exemplo: no caso acima precisamos reorganizar os valores em ordem crescente: 11,11,12,13,14,15,16,18,19 Com os valores reorganizados, percebe-se que a mediana é 14. |
É o valor que mais aparece em um conjunto de dados.
Exemplo: O valor que mais se repete no conjunto acima é o 11.
|

- Moda: Em alguns conjuntos de dados pode haver mais de um termo se repetindo dentro dele e nomeamos esses eventos: – Bimodal: dois termos diferentes se repetem na mesma quantidade. Exemplo: 1,1,5,4,7,3,4. As modas são 1 e 4. – Trimodal: três termos diferentes se repetem na mesma quantidade. Exemplo: 2,4,6,5,3,6,2,5,9. As modas são 2,5 e 6. – Multimodal: quatro ou mais termos diferentes se repetem na mesma quantidade. Exemplo: 5,7,2,9,3,6,6,1,8,3,7,2,9. As modas são 2,3,7 e 9.
- Mediana: No primeiro exemplo foi simples encontrar a mediana por quê temos uma quantidade ímpar de termos (9). Mas o que fazemos quando o conjunto tiver termos em quantidade par? Bom, pense no seguinte conjunto:
2,4,6,8,10,12
Temos 6 termos, não tem um central, o que fazemos? Em casos como este pegamos os 2 números centrais e tiramos a média entre eles
6+8÷2=7
Portanto, a mediana desse conjunto é 7. Loucura né?!
| Variância | Desvio Padrão |
|
A variância mede o quanto os números de um conjunto se afastam da média. Se todos os números forem iguais teremos uma variância = 0. Quanto mais diferentes os números forem da média, maior será a variância.
Conjunto: 2, 4, 6 Média: (2+4+6)÷3=4 Diferença de cada termo em relação à média: 2-4=-2, 4-4=0, 6-4=2 O quadrado da diferença: (-2)²=4, 0²=0, 2²=4 Variância: (4+0+4)÷3=2 |
O desvio padrão é a raiz quadrada da variância, voltando para a mesma unidade dos dados. Ele também indica o quanto os dados estão distantes da média, mas de forma mais intuitiva.
Exemplo: Variância = 2 Desvio Padrão = √2 ≅ 1,41
|
Agora que entendemos a teoria, vamos visualizar como aplicamos esses conceitos em prática a seguir:
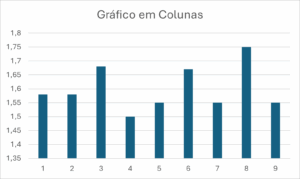
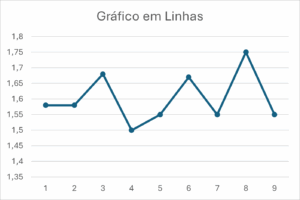
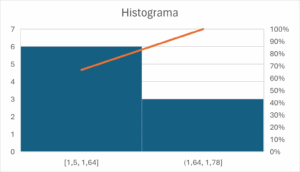
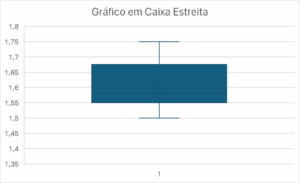
Exemplo 1: Um professor mediu a altura (em metros) de 9 estudantes de uma turma:
1,58; 1,58; 1,68; 1,50; 1,55; 1,67; 1,55; 1,75; 1,55
Com base nesses dados, determine:
- Média aritmética das alturas.
- Mediana das alturas.
- Moda das alturas.
- Variância das alturas.
- Desvio padrão das alturas.
Resolução 1:
1. Me = ∑xi÷N = (1,58+1,58+1,68+1,50+1,55+1,67+1,55+1,75+1,55)÷9 ≈ 1,60 m
2. Ordenando: 1,50; 1,55; 1,55; 1,55; 1,58; 1,58; 1,67; 1,68; 1,75
(ímpar) ⇒ a mediana é o 5º valor da lista ordenada.
5º valor = 1,58 m.
3. Frequências: 1,55 (3 vezes), 1,58 (2, portanto,
Moda = 1,55 m.
4. Média = 1,60m
Diferença de cada termo em relação à média e o quadrado das diferenças:
1,50-1,60 = -0,101 -> (-0,101)²= 0,010221
1,55-1,60 = -0,051 -> (-0,051)²= 0,002611
1,55-1,60 = -0,051 -> (-0,051)²= 0,002611
1,55-1,60 = -0,051 -> (-0,051)²= 0,002611
1,58-1,60 = -0,021 -> (-0,021)²= 0,000445
1,58-1,60 = -0,021 -> (-0,021)²= 0,000445
1,67-1,60 = 0,069 -> (0,069)²= 0,004744
1,68-1,60 = 0,079 -> (0,079)²= 0,006223
1,75-1,60 = 0,149 -> (0,149)²= 0,022171
σ² = ∑(xi−Me)²÷N = (0,010221+0,002611+0,002611+0,002611+0,000445+0,000445+0,004744+0,006223+0,022171)÷9 ≈ 0,0057869 m²
5.σ = √σ² = √0,0057869 ≈ 0,076 m
Exemplo 2: Analise a tabela a seguir
| Estudante | Altura (m) |
| 1 | 1,58 |
| 2 | 1,65 |
| 3 | 1,70 |
| 4 | 1,75 |
| 5 | 1,62 |
| 6 | 1,80 |
| 7 | 1,68 |
| 8 | 1,75 |
| 9 | 1,72 |
| 10 | 1,68 |
| 11 | 1,74 |
| 12 | 1,65 |
Agora responda:
- Calcule média, mediana e moda das alturas.
- Calcule variância e desvio padrão.
- Compare os resultados: a turma apresenta grande dispersão de alturas ou os alunos são relativamente homogêneos?
Resolução 2:
1. Média:
Me =∑xi÷N= (1,58+1,65+1,70+1,75+1,62+ 1,80+ 1,68+ 1,75+ 1,72+ 1,68+ 1,74+ 1,65)÷12 ≈ 1,693 m
Mediana:
Ordenando: 1,58; 1,62; 1,65; 1,65; 1,68; 1,68; 1,70; 1,72; 1,74; 1,75; 1,75; 1,80
⇒ média entre o 6º e 7º valores.
6º = 1,68; 7º = 1,70 ⇒ 1,68+1,70÷2=1,69 m
Moda: 1,65; 1,68; 1,75 (todas aparecem 2x) ⇒ trimodal.
2.
1,58-1,693 = -0,113 -> (-0,113)²= 0,012769
1,62-1,693 = -0,073 -> (-0,073)²= 0,005329
1,65-1,693 = -0,043 -> (-0,043)²= 0,001849
1,65-1,693 = -0,043 -> (-0,043)²= 0,001849
1,68-1,693 = -0,013 -> (-0,013)²= 0,000169
1,68-1,693 = -0,013 -> (-0,013)²= 0,000169
1,70-1,693 = 0,007 -> (0,007)²= 0,0049
1,72-1,693 = 0,027 -> (0,027)²= 0,000729
1,74-1,693 = 0,047 -> (0,047)²= 0,002209
1,75-1,693 = 0,057 -> (0,057)²= 0,003249
1,75-1,693 = 0,057 -> (0,057)²= 0,003249
1,80-1,693 = 0,107 -> (0,107)²= 0,011449
σ² = ∑(xi−Me)²÷N = (0,012769+0,005329+0,001849+0,001849+0,000169+0,000169+0,0049+0,000729+0,002209+0,003249+0,003249+0,011449)÷9 ≈ 0,00399325 m²
σ = √σ² = √0,00399325 ≈ 0,063 m
3. Ao observar os cálculos anteriores, notamos que a média das alturas representa bem o grupo, pois a maioria dos valores está próxima dela. A mediana e a moda também ficaram muito próximas da média, indicando que não há grandes distorções causadas por valores extremos (ou seja, não há outliers que puxem os resultados para cima ou para baixo).
Quando analisamos a variância e o desvio padrão, percebemos que os valores encontrados são relativamente baixos em relação à média das alturas. Isso significa que as diferenças entre os estudantes não são tão grandes: a maioria apresenta altura próxima do valor central.
Portanto, a turma pode ser considerada relativamente homogênea em relação à altura. Existe uma pequena variação natural — como esperado em qualquer grupo de pessoas — mas essa variação não é suficiente para caracterizar grande dispersão.
Vamos trazer um exemplo real do uso da estatística em vestibulares. A seguir, questão 162 do caderno verde do ENEM 2024:

Resolução
-
Organizar os dados em ordem crescente:
46, 54, 60, 64, 64, 66. -
Mediana (medida de posição):
Como há número par de observações (6), a mediana é a média aritmética dos dois valores centrais (3º e 4º): mediana=60+64
Resposta correta: 62 (alternativa E). -
Medidas adicionais úteis para estatística descritiva
-
Média (tendência central):
Soma dos valores =66+64+54+46+60+64÷6=59 -
Moda: 64 (aparece duas vezes; os outros aparecem uma vez).
-
Variância populacional e desvio padrão:
Desvios em relação à média 59:.
Quadrados: 49,25,25,169,1,25Soma dos quadrados: 294.
Variância populacional: 294÷6=49Desvio padrão populacional: √49=7
-
Em um conjunto de dados, as medidas de tendência central — média, mediana e moda — são utilizadas para representar o valor típico ou central de uma distribuição. Entretanto, esses indicadores podem apresentar resultados diferentes dependendo da distribuição dos valores e da presença de extremos (valores muito altos ou muito baixos).
No exemplo analisado, os dados de umidade relativa do ar (66, 64, 54, 46, 60 e 64) apresentaram média igual a 59, mediana igual a 62 e moda igual a 64. Observa-se que a média ficou menor que a mediana, o que indica uma distribuição assimétrica à esquerda, ou seja, puxada por valores menores. Nesse caso, o valor 46, que é significativamente mais baixo que os demais, exerce forte influência sobre a média, reduzindo-a.
A mediana, por sua vez, é menos afetada por valores extremos, pois depende apenas da posição dos dados ordenados, e não da magnitude de todos eles. Por isso, a mediana (62) representa melhor o comportamento típico do conjunto. Já a moda (64) indica o valor mais frequente, reforçando a concentração dos dados próximos a esse número.
Portanto, a comparação entre essas três medidas mostra como a presença de um valor atípico (46) altera a média, mas mantém a mediana e a moda praticamente inalteradas, evidenciando a importância de analisar mais de uma medida para descrever corretamente um conjunto de dados.
