Função Polinomial do 1° Grau
Ao coletarmos dados que variam linearmente podemos construir uma reta que irá representar essa relação e é por meio dela que será possível prever valores que seguem o mesmo tipo de variação. Para isso, torna-se necessário conhecermos as propriedades e características da função do 1° grau.
Definição
A forma básica para uma função de 1° grau (ou função afim) deverá sempre seguir o formato abaixo:
[math] f(x) = ax + b, com\ a \ \epsilon \ \mathbb{R}^* e \ b \ \epsilon \ \mathbb{R}[/math]
Exemplos:
a) [math] g:\mathbb{R}\to \mathbb{R},g(x)=4x+5[/math]
b) [math] f:\mathbb{R}^+\to \mathbb{R}^+,f(x)=-9x+12[/math]
c) [math] h:\mathbb{R}^*\to \mathbb{R},h(x)=8x[/math]
Gráfico
O gráfico da função afim, sempre será uma reta. Para ser possível traçar uma reta é necessário que tenhamos ao menos 2 pontos definidos. O gráfico da função afim sempre seguirá o formato abaixo:
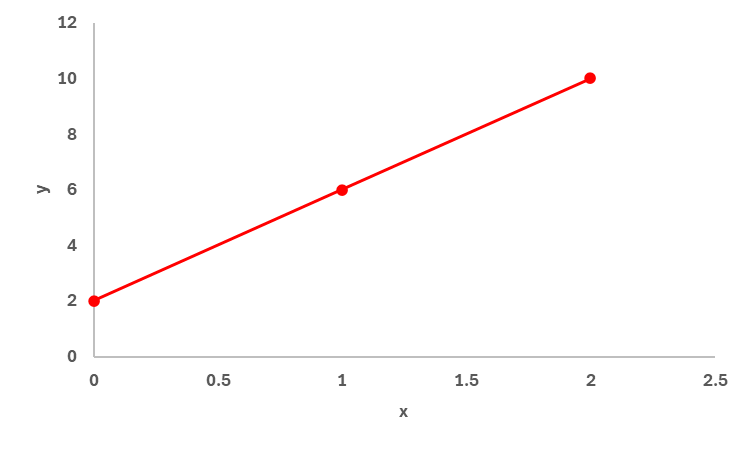
Exemplo – Construção do Gráfico
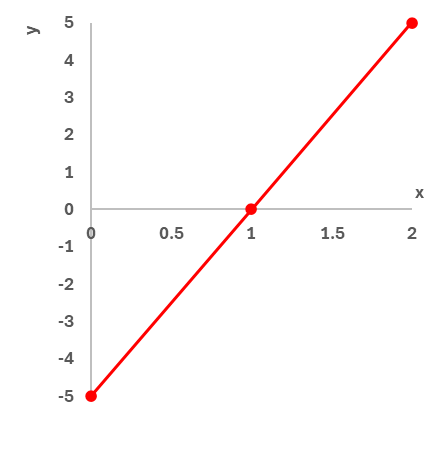
Suponha que temos a função: [math] f:\mathbb{R}\to \mathbb{R},y=5x-5[/math],
Se substituirmos o valor de x podemos encontrar valores de y que se relacionam com ele. Por exemplo,
- Para [math]x = 0[/math], temos [math]y = 5×0 – 5 = -5[/math] ⭢ [math]A( 0,-5)[/math]
- Para [math]x = 1[/math], temos [math]y = 5×1 – 5 = 0[/math] ⭢ [math]B( 1,0)[/math]
- Para [math]x = 2[/math], temos [math]y = 5×2 – 5 = 5[/math] ⭢ [math]B( 2,5)[/math]
Com os dados obtidos torna-se possível montar uma tabela e a partir dela construir nosso gráfico:
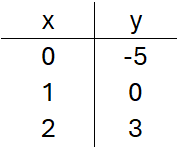
Termos da Função Afim
Vamos analisar agora os termos que compões a função afim:
[math]y = a . x + b[/math]
Temos que, a e b são coeficientes numéricos e que y e x são nossas incógnitas.
Coeficiente Linear
O termo independente b (b ∈ ℝ), é chamado de coeficiente linear da função afim. Ele pode ser obtido se considerarmos [math]a=0[/math] ou então analisando onde a linha traça o eixo das ordenadas, ou seja, ponto (0,b)
!!Atenção!! Se [math]b=0[/math], temos que [math]f(x)=ax[/math] e podemos chamar de função linear.
Exemplos:
a) [math]y = 5x – 5[/math], temos que [math]b= -5[/math]
b) [math]y = -8x + 10[/math], temos que [math]b=10[/math]
Coeficiente Angular
O coeficiente angular portanto é o coeficiente a da função ([math]y = a . x + b[/math]). Para entender melhor o que é o coeficiente angular, vamos analisar o gráfico da função
[math]y = 2x + 1[/math] abaixo, em que [math]a=2[/math]:
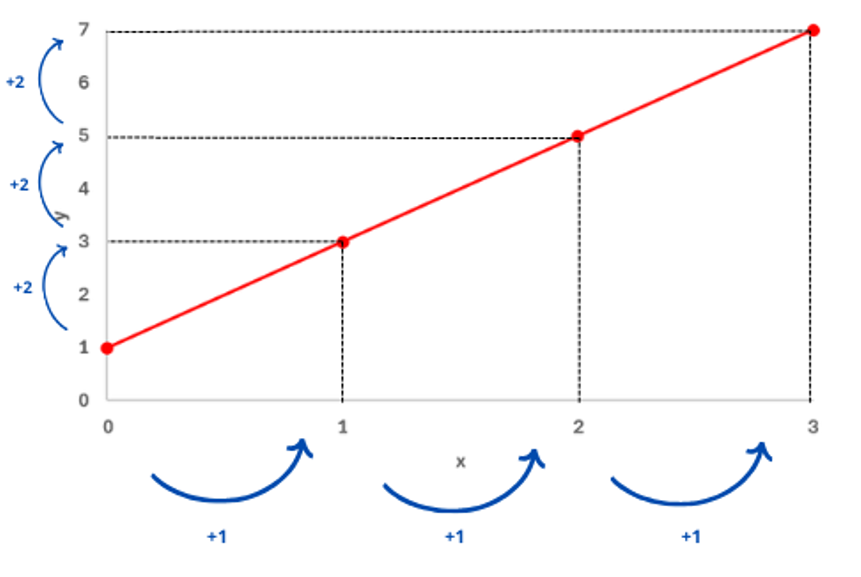
Nota-se que a cada aumento de 1 unidade no eixo x tem-se o aumento de 2 unidades no eixo y, essa relação corresponde ao coeficiente angular da nossa função.
Portanto, podemos fazer algumas análises sobre o valor do coeficiente angular.
- Se [math]a>0[/math]⭢ Função crescente
- Se [math]a<0[/math] ⭢ Função decrescente
Com isso, podemos afirmar que o coeficiente angular mede a variação dos valores de y em relação aos valores de x. Esse coeficiente também pode ser calculado da seguinte maneira:
Dados dois pontos (x1,y1) e (x2,y2): [math]a = \frac{\Delta y}{\Delta x}[/math] , ou seja, [math]a =\frac{(y2-y1)}{(x2-x1)}[/math]
Exercícios Resolvidos
Exercício 1: Calcule o coeficiente angular da função do 1° grau que passa pelos pontos abaixo e verifique se a função é crescente ou decrescente: a) A(1,5) e B(3,11) b) C(4,10) e D(7,5)
Resolução
a) [math]a =\frac{(yb – ya)}{(xb – xa)}[/math] ⭢ [math]a =\frac{(11-5)}{(3-1)}[/math] ⭢ [math]a = 3[/math]; [math]a>0[/math] ⭢ função crescente
b) [math]a = \frac{(yd – yc)}{(xd – xc)}[/math] ⭢ [math]a = \frac{(5-10)}{(7-4)}[/math] ⭢ [math]a = \frac{-5}{3}[/math]; [math]a<0[/math] ⭢ função decrescente
Exercício 2: Defina a função do 1° grau que passa pelos pontos (2,-1) e (4,3).
Resolução
Como vimos anteriormente, a função do 1° grau possui a forma [math]y = a . x + b[/math], com isso temos:
[math](2,-1)[/math] ⭢ [math]-1 = a . 2 + b[/math] ⭢ [math]2a + b = -1[/math] (I)
[math](4,3)[/math] ⭢ [math]3 = a . 4 + b[/math] ⭢ [math]4a + b = 3[/math] (II)
Subtraindo (I) em (II), temos: [math]2a = 4[/math] ⭢ [math]a = 2[/math]
Substituindo [math]a=2[/math] em (I): [math]2 . 2 + b = -1[/math] ⭢ [math]b = -5[/math]
Portanto a função é [math]y = 2 x – 5[/math]
Raiz da função
A raiz da função do 1° grau é o valor em que x “bate” no eixo das abscissas. Nesse ponto, sabemos que [math]y=0[/math].
Exemplo:
- [math]y = 2x – 10[/math], para [math]y=0[/math] temos [math]2x-10 = 0[/math], nesse caso [math]x=5[/math] (raiz da função)
- [math]y=4x+12[/math], para [math]y=0[/math] temos [math]4x+12=0[/math], nesse caso [math]x=-3[/math] (raiz da função)
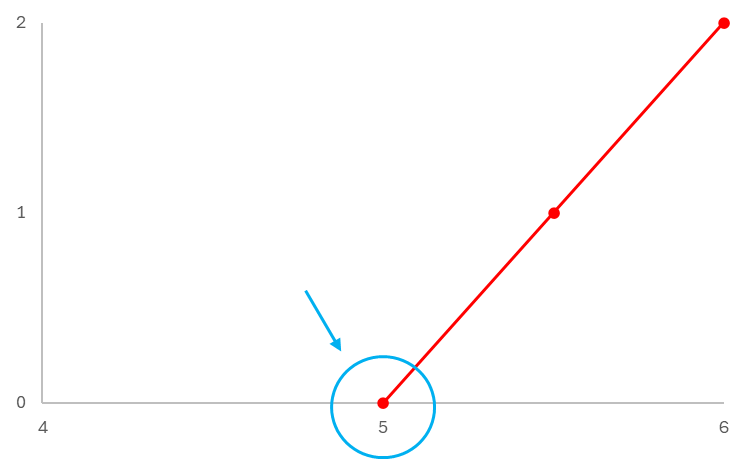
Visualização da raiz em gráficos
Vamos analisar a raiz da função [math]y = 2x + 10[/math], em que a raiz é [math]x=5[/math] .
Análise do sinal de uma função
Analisar o sinal de uma função é o mesmo de analisar o sinal da variável y para os intervalos de x. Quando o gráfico está acima do eixo x (eixo das absicissas), podemos afirmar que a função assume valores positivos, já quando está abaixo desse eixo assume valores negativos.
Se conhecermos a raiz e o sinal do coeficiente angular da função já podemos concluir o estudo do sinal da mesma. Por exemplo,
a) [math]y = 2 x – 8[/math]
Sabemos que a é o seu coeficiente angular, nesse caso [math]a=2[/math], então concluímos que é uma função crescente.
Para encontrarmos a raiz da função, basta substituir [math]y=0[/math], dessa forma encontramos que a raiz é [math]x=4[/math].
Montando o gráfico, temos o caso abaixo:
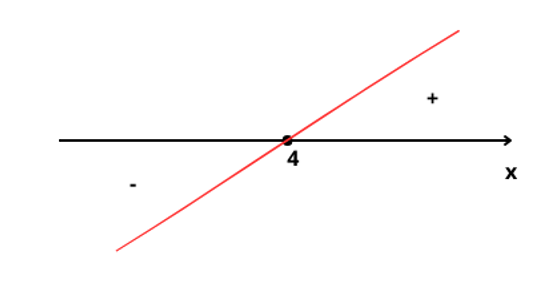
Assim, o estudo do sinal da função, será:
se [math]x>4[/math], então [math]y>0[/math]
se [math]x=4[/math], então [math]y=0[/math]
se [math]x<4[/math], então [math]y<0[/math]
Grandezas proporcionais
Ao obtermos pares ordenados (x,y) que relacionam duas grandezas, se as razões x/y forem sempre igual, podemos afirmar que são grandezas diretamente proporcionais.
Por exemplo, se uma lanchonete vende lanches a R$ 6,00, a quantidade de lanches comprados e o valor a ser pago por eles são grandezas diretamente proporcionais. Veja,

Nota-se que [math]\frac{1}{6} =\frac{2}{12} =\frac{3}{18} =…[/math], ou seja, as razões x/y são constantes.
Agora, caso a mesma lanchonete começasse a cobrar uma taxa extra de R$ 5,00 de estacionamento, para quem fosse de carro, os novos valores seriam:

Nesse caso, nota-se que [math]\frac{1}{11}\neq \frac{1}{17}\neq \frac{3}{23}\neq \frac{4}{29}…[/math], ou seja, as razões x/y NÃO são mais constantes.
Desse modo pode-se afirmar que as grandezas NÃO são proporcionais. Porém, se analisarmos as variações Δx e Δy, são, mas por que?
Se considerarmos a razão entre a variação de doces e a variação de valores a pagar temos um valor constante de 1/6:
[math]\frac{(2-1)}{(17-11)} =\frac{(3-2)}{(23-17)} =\frac{(4-3)}{(29-23)} =…=\frac{1}{6}[/math]
Ou seja, a cada aumento de uma unidade, a conta aumenta R$ 6,00.
