Números complexos: Forma Algébrica
Números complexos: Forma Algébrica
Os números complexos, bem como os números reais, em essência, podem ser representados de duas formas: algébrica e geométrica. Vamos, aqui, nos ater à representação algébrica de um número complexo.
Primeiro, vamos entender o que são os números complexos. Historicamente, os números complexos surgiram como uma solução para o problema matemático [math]\sqrt{-1}[/math]. Pense em algum número real que, elevado a ele mesmo, resulte em um número negativo. Por mais que você tente, nunca vai encontrá-lo.
O matemático italiano Raffaele Bombelli foi o primeiro a introduzir a notação [math]i = \sqrt{-1}[/math] e a utilizar esse conceito para trabalhar com equações polinomiais de grau 3. Posteriormente, os números complexos foram empregados para encontrar soluções de equações polinomiais que não possuíam solução dentro do conjunto dos números reais.
Desde então, surgiu a necessidade de expandir o conjunto dos números reais e, assim, um novo conjunto numérico foi criado: o conjunto dos números complexos!
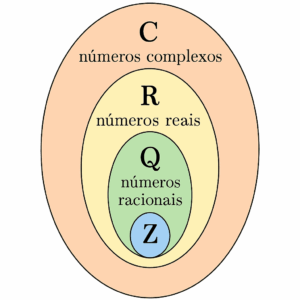
Definimos um número complexo genérico como: [math]{z} = a+bi [/math], onde a é definida como a parte real do número complexo e bmultiplicado por [math]\sqrt{-1}[/math] é chamada de parte complexa. Sendo assim, qualquer número real pode ser representado pela notação [math]{z} = a+bi[/math], onde b= 0.
Por exemplo:
- 2 = 2 + 0.i
- 5= 5 + 0.i
Agora que sabemos como representar os números complexos em sua forma algébrica, vamos mais a fundo explorar suas propriedades!
Primeiro, vamos aqui estudar o conjugado de um número complexo, definido por:
- [math]\overline{z}= a-bi[/math]
Vamos agora estudar
Soma:
[math]{(a+bi)}+{(c+di)} = {(a+c)} + {(d+b)i}[/math]
Ou seja, quando tratamos da soma entre dois números complexos, devemos somar suas partes reais e depois suas partes imaginárias, nunca podemos somar a parte real com a parte imaginária, pois, lembremos, são operações entre conjuntos diferentes. A parte complexa dos números complexos não está contidos nos reais.
Subtração:
[math]{(a+bi)}-{(c+di)} = {(a-c)} +{(b-d)i}[/math]
Empregamos a mesma ideia quando vamos subitrair dois números complexos. Subtraimos as partes reais, depois, somamos a subtração da parte imaginária
Multiplicação:
Dado dois números complexos em forma algébrica:
[math] z_1 = a + bi \quad \text{e} \quad z_2 = c + di [/math]
A multiplicação entre eles é feita aplicando a propriedade distributiva da multiplicação (ou produto notável), lembrando sempre que:
[math] i^2 = -1 [/math]
Assim:
[math] z_1 \cdot z_2 = (a + bi)(c + di) [/math]
Efetuando a multiplicação termo a termo, temos:
[math] z_1 \cdot z_2 = ac + adi + bci + bdi^2 [/math]
Substituindo [math] i^2 = -1 [/math]:
[math] z_1 \cdot z_2 = ac + adi + bci – bd [/math]
Agrupando as partes reais e imaginárias:
[math] z_1 \cdot z_2 = (ac – bd) + (ad + bc)i [/math]
Portanto, o produto de dois números complexos é dado por:
[math] (a + bi)(c + di) = (ac – bd) + (ad + bc)i [/math]
Divisão:
Para dividir dois números complexos, multiplicamos numerador e denominador pelo conjugado do denominador.
Dado:
[math] \frac{z_1}{z_2} = \frac{a + bi}{c + di} [/math]
Multiplicamos o numerador e o denominador pelo conjugado de [math] z_2 [/math]:
[math] \frac{a + bi}{c + di} \cdot \frac{c – di}{c – di} [/math]
Efetuando o produto:
[math] \frac{(a + bi)(c – di)}{(c + di)(c – di)} [/math]
No denominador, aplicamos o produto da soma pela diferença:
[math] (c + di)(c – di) = c^2 – (di)^2 = c^2 + d^2 [/math]
No numerador:
[math] (a + bi)(c – di) = ac – adi + bci – bdi^2 [/math]
[math] = (ac + bd) + (bc – ad)i [/math]
Logo:
[math] \frac{a + bi}{c + di} = \frac{(ac + bd) + (bc – ad)i}{c^2 + d^2} [/math]
Separando as partes real e imaginária:
[math] \frac{a + bi}{c + di} = \frac{ac + bd}{c^2 + d^2} + \frac{bc – ad}{c^2 + d^2}i [/math]
Exercícios de aplicação
(Unesp-SP) Se z = (2 + i) ∙ (1 + i) ∙ i, então z, o conjugado de z, será dado por ?
Resolução:
[math] z = (2 + i)(1 + i)i [/math]
Primeiro, desenvolvemos a multiplicação entre os dois primeiros fatores:
[math] (2 + i)(1 + i) = 2(1) + 2(i) + i(1) + i(i) = 2 + 2i + i + i^2 [/math]
Sabendo que [math] i^2 = -1 [/math], temos:
[math] 2 + 3i – 1 = 1 + 3i [/math]
Logo:
[math] (2 + i)(1 + i) = 1 + 3i [/math]
Agora multiplicamos o resultado por [math] i [/math]:
[math] z = (1 + 3i)i = i + 3i^2 = i – 3 [/math]
Portanto:
[math] z = -3 + i [/math]
O conjugado de [math] z [/math], indicado por [math] \overline{z} [/math], é obtido trocando o sinal da parte imaginária:
[math] \overline{z} = -3 – i [/math]
(UFU-MG) Sejam os complexos z = 2x – 3i e t = 2 + yi, onde x e y são números reais. Se z = t, então o produto x.y é ?
Resolução:
Temos:
[math] z = 2x – 3i \quad \text{e} \quad t = 2 + yi [/math]
Sabemos que se [math] z = t [/math], então suas partes reais e partes imaginárias são iguais.
Assim:
Parte real de [math] z [/math] é [math] 2x [/math], e parte real de [math] t [/math] é [math] 2 [/math].
Logo:
[math] 2x = 2 \Rightarrow x = 1 [/math]
Parte imaginária de [math] z [/math] é [math] -3 [/math], e parte imaginária de [math] t [/math] é [math] y [/math].
Logo:
[math] -3 = y \Rightarrow y = -3 [/math]
O problema pede o produto [math] x \cdot y [/math]:
[math] x \cdot y = 1 \cdot (-3) = -3 [/math]
