Números Complexos: Forma Geométrica

 

Números complexos: Forma Geométrica

Os números complexos, bem como os números reais, em essência, podem ser representados de duas formas: algébrica e geométrica. Vamos, aqui, nos ater à representação geométrica de um número complexo.

Primeiro, vamos entender a necessidade dessa representação. Historicamente, após a consolidação dos números complexos por meio da forma algébrica [math] z = a + bi [/math], onde [math] a [/math] e [math] b [/math] são números reais e [math] i [/math] é a unidade imaginária, surgiu um questionamento: como visualizar um número que possui uma parte “real” e outra “imaginária”?

A genialidade para a solução desse problema veio dos trabalhos independentes dos matemáticos Caspar Wessel, Jean-Robert Argand e, posteriormente, Carl Friedrich Gauss. Eles propuseram que um número complexo [math] a + bi [/math] poderia ser representado não em uma reta numérica, como os reais, mas em um plano. Surgia assim o que hoje chamamos de Plano de Argand-Gauss.

Neste plano, o eixo horizontal (eixo x) representa a parte real do número complexo, enquanto o eixo vertical (eixo y) representa a parte imaginária. Dessa forma, o número complexo [math] z = a + bi [/math] corresponde ao ponto [math] (a, b) [/math] ou ao vetor que vai da origem [math] (0, 0) [/math] até esse ponto.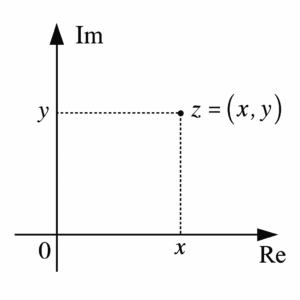

No Plano de Argand-Gauss, cada número complexo [math] z = a + bi [/math] é representado por um ponto de coordenadas [math] (a, b) [/math]. A distância deste ponto até a origem é chamada de módulo do número complexo, denotado por [math] |z| [/math] e calculado por:

[math] |z| = \sqrt{a^2 + b^2} [/math]

O ângulo que o segmento entre a origem e o ponto [math] (a, b) [/math] faz com o eixo real é denominado argumento de [math] z [/math], geralmente representado por [math] \theta [/math].

Representação Polar

A partir do módulo e do argumento, podemos expressar qualquer número complexo na forma polar:

[math] z = |z|(\cos \theta + i \sin \theta) [/math]

Ou, na notação compacta:

[math] z = |z| \text{cis} \theta [/math]

Operações na Forma Geométrica

Soma e Subtração:
Geometricamente, a soma de dois números complexos corresponde à soma vetorial no plano. Se [math] z_1 = a + bi [/math] e [math] z_2 = c + di [/math], então [math] z_1 + z_2 [/math] é o vetor resultante da adição dos vetores [math] (a, b) [/math] e [math] (c, d) [/math].

Multiplicação e Divisão:
Na forma polar, a multiplicação e divisão tornam-se:

• Multiplicação: [math] z_1 \cdot z_2 = |z_1||z_2| \text{cis}(\theta_1 + \theta_2) [/math]
  Os módulos se multiplicam e os argumentos se somam.

Divisão: [math] \frac{z_1}{z_2} = \frac{|z_1|}{|z_2|} \text{cis}(\theta_1 – \theta_2) [/math]
Os módulos se dividem e os argumentos se subtraem.                         

Conjugado Complexo Geometricamente
O conjugado [math] \overline{z} = a – bi [/math] é representado pelo ponto [math] (a, -b) [/math], que é o reflexo do ponto [math] (a, b) [/math] em relação ao eixo real.

Potenciação e Radiciação
A forma polar é especialmente útil para potenciação e radiciação:

Fórmula de De Moivre: [math] z^n = |z|^n \text{cis}(n\theta) [/math]

Raiz n-ésima: [math] \sqrt[n]{z} = \sqrt[n]{|z|} \text{cis}\left(\frac{\theta + 2k\pi}{n}\right) [/math] para [math] k = 0, 1, 2, …, n-1 [/math]

Exercícios de aplicação

1)Dados os números complexos z1 = (2, -1) e z2 = (3 , x), sabe-se que z1 ⋅ z2 ∈ R. Então x é igual a

a) − 6.
b) − 3/2.
c) 0.
d) 3/2.
e) 6.

[math]
\text{Dados } z_1 = 2 – i \text{ e } z_2 = 3 + xi,\ \text{sabemos que } z_1 z_2 \in \mathbb{R}.
[/math]

[math]
z_1 z_2 = (2 – i)(3 + xi)
[/math]

[math]
z_1 z_2 = 6 + 2xi – 3i – xi^2
[/math]

[math]
z_1 z_2 = 6 + x + (2x – 3)i
[/math]

Para que o produto seja real, a parte imaginária deve ser nula:

[math]
2x – 3 = 0
[/math]

[math]
x = \frac{3}{2}
[/math]

2) Considere os números complexos [math] z_1 = (1, 2) [/math] e [math] z_2 = (k, -1) [/math], com [math] k \in \mathbb{R} [/math], representados no Plano de Argand-Gauss.

Sabe-se que o quociente [math] \frac{z_1}{z_2} [/math] é um número puramente imaginário, isto é, sua parte real é nula.

Então, o valor de [math] k [/math] é:

a) −2
b) −1
c) 0
d) 1
e) 2

Resolução

Primeiro, escrevemos [math] z_1 [/math] e [math] z_2 [/math] na forma algébrica:

[math] z_1 = 1 + 2i [/math]
[math] z_2 = k – i [/math]

Queremos que:

[math] \frac{z_1}{z_2} \text{ seja puramente imaginário} [/math]

Isto é, a parte real deve ser zero.

Calculamos o quociente:

[math] \frac{z_1}{z_2} = \frac{1 + 2i}{k – i} [/math]

Multiplicamos numerador e denominador pelo conjugado do denominador:

[math] \frac{1 + 2i}{k – i} \cdot \frac{k + i}{k + i} = \frac{(1 + 2i)(k + i)}{(k – i)(k + i)} [/math]

Denominador:

[math] (k – i)(k + i) = k^2 + 1 [/math]

Numerador:

[math] (1 + 2i)(k + i) = k – 2 + (1 + 2k)i [/math]

Assim, o quociente é:

[math] \frac{z_1}{z_2} = \frac{(k – 2) + (1 + 2k)i}{k^2 + 1} [/math]

Separando em parte real e imaginária:

[math] \frac{z_1}{z_2} = \frac{k – 2}{k^2 + 1} + \frac{1 + 2k}{k^2 + 1} i [/math]

Para que o número seja puramente imaginário, a parte real deve ser nula:

[math] \frac{k – 2}{k^2 + 1} = 0 [/math]

Como o denominador é sempre positivo:

[math] k – 2 = 0 [/math]

[math] k = 2 [/math]

Portanto, a resposta correta é:

[math] \boxed{2} [/math]

Alternativa e).