Números Complexos: Identidades Trigonométricas
Números Complexos: Identidades Trigonométricas
Os números complexos, quando representados na forma polar, apresentam uma relação direta com a trigonometria. Essa correspondência permite a dedução e demonstração de diversas identidades trigonométricas por meio de propriedades algébricas.
Representação Geométrica e o Círculo Trigonométrico
Um número complexo [math] z = a + bi [/math] pode ser representado por um ponto [math] P(a, b) [/math] no plano complexo, também chamado de plano de Argand-Gauss.
O eixo real corresponde ao eixo das abscissas e o eixo imaginário ao das ordenadas.
O vetor de origem [math] O(0, 0) [/math] até o ponto [math] P(a, b) [/math] representa o número complexo.
Seu comprimento é o módulo do número complexo:
[math] |z| = \sqrt{a^2 + b^2} [/math]
O ângulo [math] \theta [/math], formado entre o vetor [math] \overrightarrow{OP} [/math] e o eixo real positivo, é o argumento de [math] z [/math].
No círculo trigonométrico, que é o círculo de raio unitário ([math] r = 1 [/math]) centrado na origem, cada ponto tem coordenadas:
[math] (\cos \theta, \sin \theta) [/math]
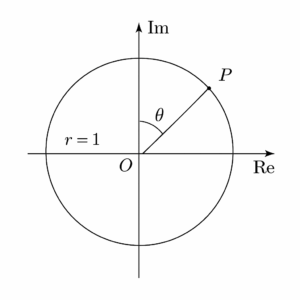
Assim, um número complexo de módulo 1 pode ser escrito como:
[math] z = \cos \theta + i \sin \theta [/math]
Quando o módulo é diferente de 1, o ponto correspondente é obtido multiplicando o raio unitário pelo módulo [math] |z| [/math]:
[math] z = |z|(\cos \theta + i \sin \theta) [/math]
Essa representação geométrica estabelece a base para a forma polar e a interpretação trigonométrica dos números complexos.
Forma Polar e Fórmula de Euler
Um número complexo pode ser expresso na forma polar como:
[math] z = |z|(\cos \theta + i \sin \theta) [/math]
A Fórmula de Euler estabelece a equivalência entre a forma trigonométrica e a exponencial:
[math] e^{i\theta} = \cos \theta + i \sin \theta [/math]
Portanto, a forma exponencial de um número complexo é:
[math] z = |z| e^{i\theta} [/math]
Demonstração de Identidades com Números Complexos
Fórmulas de Adição
Considere dois números complexos na forma exponencial:
[math] e^{i\alpha} \quad \text{e} \quad e^{i\beta} [/math]
O produto é dado por:
[math] e^{i\alpha} \cdot e^{i\beta} = e^{i(\alpha + \beta)} [/math]
Aplicando a Fórmula de Euler em ambos os lados:
Lado Esquerdo:
[math] (\cos \alpha + i \sin \alpha)(\cos \beta + i \sin \beta) = (\cos \alpha \cos \beta – \sin \alpha \sin \beta) + i(\cos \alpha \sin \beta + \sin \alpha \cos \beta) [/math]
Lado Direito:
[math] \cos(\alpha + \beta) + i \sin(\alpha + \beta) [/math]
Comparando as partes reais e imaginárias:
Parte real:
[math] \cos(\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta [/math]
Parte imaginária:
[math] \sin(\alpha + \beta) = \cos \alpha \sin \beta + \sin \alpha \cos \beta [/math]
Fórmulas de Arco Duplo
Pela Fórmula de De Moivre, vista na parte geométrica dos números complexos:
[math] (\cos \theta + i \sin \theta)^n = \cos(n\theta) + i \sin(n\theta) [/math]
Para [math] n = 2 [/math]:
[math] (\cos \theta + i \sin \theta)^2 = \cos(2\theta) + i \sin(2\theta) [/math]
Expandindo o lado esquerdo:
[math] (\cos \theta + i \sin \theta)^2 = (\cos^2 \theta – \sin^2 \theta) + i(2 \cos \theta \sin \theta) [/math]
Igualando as partes correspondentes:
Parte real:
[math] \cos(2\theta) = \cos^2 \theta – \sin^2 \theta [/math]
Parte imaginária:
[math] \sin(2\theta) = 2 \cos \theta \sin \theta [/math]
Exercícios de aplicação
1)Um número complexo [math] z [/math] tem módulo [math] |z| = 4 [/math] e argumento [math] \theta = 150^\circ [/math].
Escreva [math] z [/math] na forma polar.
Determine [math] z [/math] na forma algébrica [math] a + bi [/math].
As alternativas para a forma algébrica são:
a) [math] z = 2\sqrt{3} + 2i [/math]
b) [math] z = -2\sqrt{3} + 2i [/math]
c) [math] z = -2\sqrt{3} – 2i [/math]
d) [math] z = 2\sqrt{3} – 2i [/math]
e) [math] z = 4i [/math]
Resolução
Pela forma polar:
[math] z = |z|(\cos\theta + i\sin\theta) [/math]
Temos [math] |z| = 4 [/math] e [math] \theta = 150^\circ [/math], então:
[math] z = 4(\cos 150^\circ + i \sin 150^\circ) [/math]
No círculo trigonométrico:
[math] \cos 150^\circ = -\frac{\sqrt{3}}{2} [/math]
[math] \sin 150^\circ = \frac{1}{2} [/math]
Logo:
[math] z = 4\left(-\frac{\sqrt{3}}{2} + i \cdot \frac{1}{2}\right) [/math]
[math] z = -2\sqrt{3} + 2i [/math]
Forma polar:
[math] z = 4(\cos 150^\circ + i \sin 150^\circ) [/math]
Forma algébrica:
[math] z = -2\sqrt{3} + 2i [/math]
Alternativa correta: b).
