Produtos notáveis

O que é um produto notável? Antes de tudo, vamos ver o que as próprias palavras falam: produto em matemática é uma multiplicação, e notável é algo que merece um reconhecimento ou destaque. Então, pela lógica, produto notável é uma multiplicação com um certo destaque e é praticamente isso. Os produtos notáveis são expressões algébricas bem conhecidas e que aparecem com frequência na matemática, seja em polinômios ou em equações do segundo e terceiro grau. Compreende-las é de suma importância para facilitar o trabalho em algumas situações. Vamos abordar 5 produtos notáveis, sendo 3 do segundo grau e 2 do terceiro grau.

• Quadrado da soma [math] \left( a+b \right)^{2} [/math]

Com certeza um dos maiores clássicos da matemática básica: se já teve contato, provavelmente já se perguntou ou viu alguém perguntando porque [math] \left( a+b \right)^{2} [/math] não é igual a [math] a^{2}+b^{2} [/math]. E se esse site é o seu primeiro contato com produtos notáveis, provavelmente em
algum momento vai ver alguém perguntando.

Vamos começar com um pequeno exemplo, usando números, de porque [math] \left( a+b \right)^{2} \neq a^{2}+b^{2}[/math] Vamos pensar em dois números, 3 e 6, sendo do a=3 e b=6 e vamos substitui-los em [math] \left( a+b \right)^{2} = a^{2}+b^{2}[/math]

[math] \left( a+b \right)^{2} = a^{2}+b^{2}[/math]
[math]\left( 3+6 \right)^{2} = 3^{2}+6^{2}[/math]
[math]\left( 3+6 \right)^{2}=9+6[/math]

[math] \left( 81\neq 45 \right) [/math] …., viu como temos um problema aqui? As coisas não são tão simples, mas também não são difíceis, basta entendermos como elas funcionam nos produtos notáveis. Vamos analisar a expressão novamente:

[math] \left( a+b \right)^{2} [/math], de onde podemos começar? Temos um elevado ao quadrado ali, e sabemos que o elevado ao quadrado é o número (ou expressão) vezes ele mesmo. Vamos então fazer isso:
[math] \left( a+b \right)^{2} =\left( a+b \right) \times\left( a+b \right) [/math], chegamos em algo diferente, e vamos aplicar a propriedade distributiva da multiplicação [math] \left( a+b \right)\times\left( a+b \right) =a^{2}+\left(a\times b\right)+\left(a \times b\right)+ b^{2}[/math], chegamos em uma expressão muito próxima do que é o real produto notável de [math] \left( a+b \right)^{2} [/math], falta apenas agruparmos dois elementos. Duas vezes aparece o elemento [math] a\times b[/math], e então significa que temos [math]2 \times a\times b[/math]. Pronto, temos a expressão final de [math] \left( a+b \right)^{2} [/math]:
[math] \left( a+b \right)\times\left( a+b \right) =a^{2}+\left( 2 \times a\times b \right) + b^{2} [/math].

Então tem um [math] 2 \times a\times b [/math] a mais? Sim, é isso mesmo. E talvez você possa não estar entendendo tudo isso, mesmo com o exemplo numérico e algébrico. Que tal partirmos para algo mais visual? Podemos pensar na forma geométrica. Você pode estar pensando como chegaremos nisso, mas é bem simples, a potência 2 não é chamada de quadrado a toa:

Pense num quadrado de lados [math]\left( a+b \right)[/math], e aqui vão algumas observações sobre a figura:

• Nesse caso traçamos as linhas que partem dos pontos que dividem os lados em a e b até o lado oposto, e desta forma temos 4 quadriláteros.
• Todos os segmentos na, sendo N o número de 1 a 6, tem o mesmo tamanho. Analogamente, o mesmo se aplica ao bN.
• Quando for citado um quadrilátero, será na forma XYZW, sendo cada letra um dos vértices. Por exemplo, o retângulo BCHG.

Vamos para a explicação agora

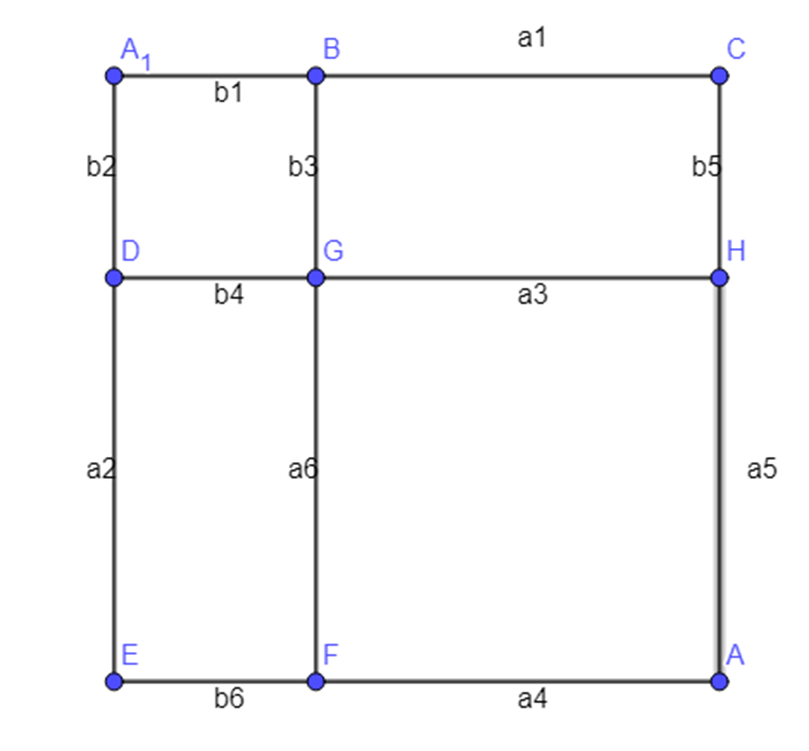
[math] \left( a+b \right)^{2} [/math] será a soma das áreas dos 4 quadriláteros que o compõe, ou seja, será a soma da área de [math] ABGD, BCHG, GHAF [/math] e [math] DGEF[/math]. Todos sabemos que a área de um quadrilátero é a multiplicação da base pela altura –[math] Área = base \times altura[/math].
Vamos começar com o quadrilátero A1BGD, cuja base vale [math]b[/math] e a altura vale [math] b [/math]. Área: [math] b \times b=b^{2}[/math]
Próximo é GHAF, cuja base vale [math]a[/math] e a altura vale [math]a[/math] . Área: [math] a\times a=a^{2}[/math]
O terceiro é BCHG, cuja base vale [math]a[/math] e altura vale [math]b[/math] . Área: [math] a\times a=ab[/math]
Por último, temos o DGEF, cuja base vale [math]b[/math] e a altura vale[math]a[/math] . Área: [math] b\times a=ba=ab[/math] (ordem dos fatores não altera o produto).
Logo a área de [math] \left( a+b \right)^{2} [/math] será: [math]a^{2}+b^{2}+ab+ab = a^{2}+b^{2}+2ab = a^{2}+2ab+b^{2}[/math], a mesma expressão encontrada pelo método algébrico. Agora ficou claro? Espero que sim.

Quadrado da diferença [math] \left( a-b \right)^{2} [/math]

O próximo item é quase igual ao anterior, dessa vez o que muda é o sinal de menos. E lembre-se, isso não é a mesma coisa que [math] a^{2}-b^{2} [/math], quando estamos trabalhando com produtos notáveis precisamos entender o que aquele produto significa. Você já passou pelo primeiro item, então deve ter uma noção do que é [math] \left( a-b \right)^{2} [/math] . Se respondeu [math]\left( a-b \right)\times \left( a-b \right)[/math], está correto. Vamos então fazer como no item anterior e aplicar a propriedade distributiva:

[math]\left( a-b \right)\left( a-b \right) = a^{2}-ab-ab+\left( (-b)(-b) \right)[/math]

Por que está [math](-b)(-b)[/math]? Apenas para visualização, já que dessa vez tem um sinal de menos no [math]b[/math]. Se multiplicarmos um número negativo por outro, teremos um número positivo, e é o que acontecerá com o [math]b[/math] nesse caso.

[math]\left( a-b \right)\left( a-b \right) = a^{2}-ab-ab+\left( (-b)(-b) \right) = a^{2}-ab-ab+b^{2}= a^{2}-2ab+b^{2}[/math]

Não foi tão difícil, não é? A única diferença é apenas o sinal de menos na frente do [math]2ab[/math].
Vamos para o terceiro tópico, que é o produto da soma pela diferença:

Produto da soma pela diferença [math]\left( a+b \right)\left( a-b \right)[/math]:

Estamos no terceiro tópico, provavelmente você já sabe o que fazer, correto? Eu escutei um aplicar a distributiva? Se sim, está corretíssimo!

[math] \left( (a+b)(a-b) \right) = a^{2}-ab+ab+b(-b) = a^{2}-b^{2}[/math]

Perceba que o [math]ab[/math] e o [math]-ab[/math] se cancelam, e o [math]b(-b)[/math] ficará com o sinal de menos na frente pois nesse caso seria apenas um sinal de menos e não dois como no anterior, fazendo aquele ficar com um sinal de positivo na frente.

“Então é dessa forma que surge o [math]a^{2}-b^{2}[/math]?” Sim, e se quiser sair de [math]a^{2}-b^{2}[/math] para [math]\left( a+b \right)\left( ab \right)[/math], também pode, desde que seja usado só o conjunto dos números reais. Vamos com o primeiro exemplo:

[math]\left( x-3 \right)\left( x-3 \right)[/math]

Tudo que mostrei é no sentido genérico, o [math]a[/math] e [math]b[/math] podem assumir qualquer valor real, e até qualquer letra.
Então vamos lá, tente fazer e veja depois a resposta:

[math]\left( x+3 \right)\left( x-3 \right) = x^{2}-3x+3x-9 = x^{2}-9[/math], fácil né?
Antes de passar mais exemplos quero mostrar a parte dos produtos notáveis do 3° grau.

Diferença de dois cubos [math]\left( a^{3}-b^{3} \right)[/math] e soma de dois cubos [math]\left( a^{3}+b^{3} \right)[/math]

Esse apenas passarei a fatoração e explicarei um macete:
[math]\left( a^{3}-b^{3} \right)[/math] =[math]\left( a-b \right)\left( a^{2}+ab+b^{2} \right)[/math]
[math]\left( a^{3}+b^{3} \right)[/math] = [math]\left( a+b \right)\left( a^{2}-ab+b^{2} \right)[/math]
O macete é o seguinte, temos 3 sinais: o do primeiro parêntese, o do [math]ab[/math] e o do [math]b^{2}[/math]
O primeiro sinal é sempre o mesmo da parte esquerda: para a diferença de quadrados será menos e para a soma será mais.
O segundo sinal, o do [math]ab[/math], será o oposto, para a diferença será mais e para assoma será menos.
O terceiro sinal, o do [math]b^{2}[/math], será SEMPRE positivo

Agora que já vimos a teoria vamos praticar um pouco!

Exercícios

1)Desenvolva os produtos notáveis.

Exemplo:

[math] \left( x+9 \right)^{2} [/math]

[math] \left(x+9\right)\left(x+9\right) = x^{2} + 9x + 9x + 81 = x^{2} +18x + 81[/math]

[math] \left( 4x-5 \right)^{2} [/math]

[math] \left( 11+y \right)^{2} [/math]

[math] \left( 2x+3y \right)^{2} [/math]

[math] \left( 2xy+2 \right)^{2} [/math]

[math] \left( 1+y \right)^{2} [/math]

[math] \left(5-y \right)^{2} [/math]

RESPOSTAS

2)Diga se é produto notável ou não.

Exemplo:

[math]\left(36-x^{2}\right)[/math]

Sim, é produto notável. [math]\left((6+x\right)\left((6-x)\right)[/math].

[math] 125 – y^{2} + 25x[/math]

[math] x^{2} – 4x + 4[/math]

[math] 2x^{2} + 9y [/math]

[math] 16x^{2} + 8x + 1[/math]

[math] 9x^{2} + 6x – 1[/math]

[math] x^{2} + 2x + 1[/math]

[math] 9x^{2} + 24xy + 16y^{2}[/math]

RESPOSTAS