Seno, Cosseno e Tangente no Círculo Trigonométrico
Seno, Cosseno e Tangente podem ser determinados como razões entre dois lados de um triângulo retângulo, mas a forma mais completa do estudo destas ferramentas é com a utilização do círculo trigonométrico e é dessa forma que abordaremos este assunto aqui!
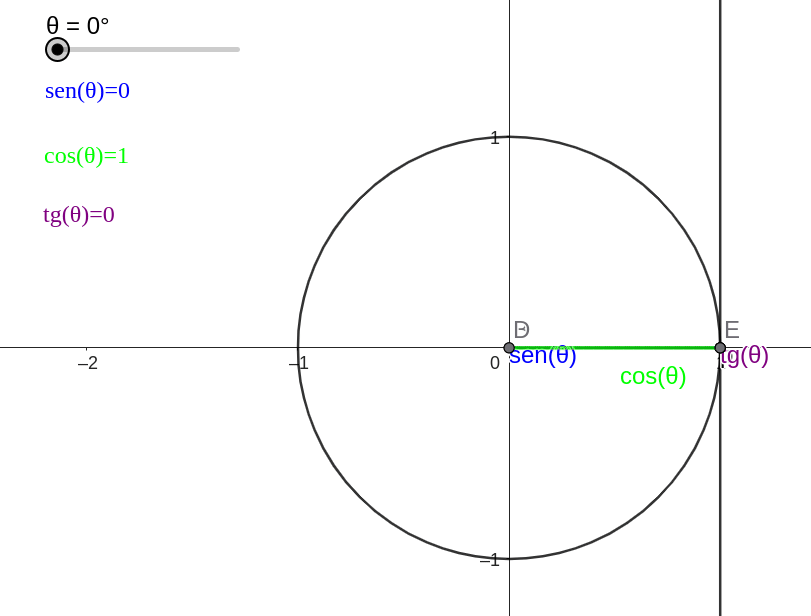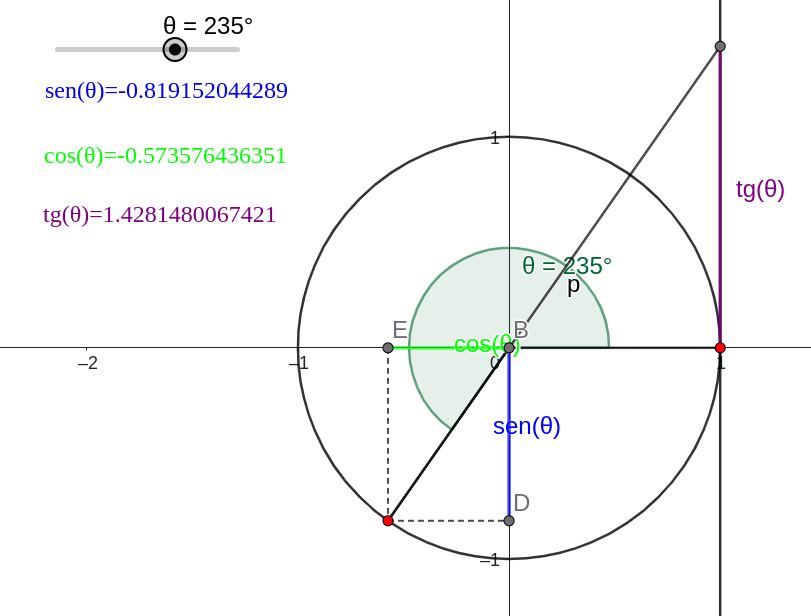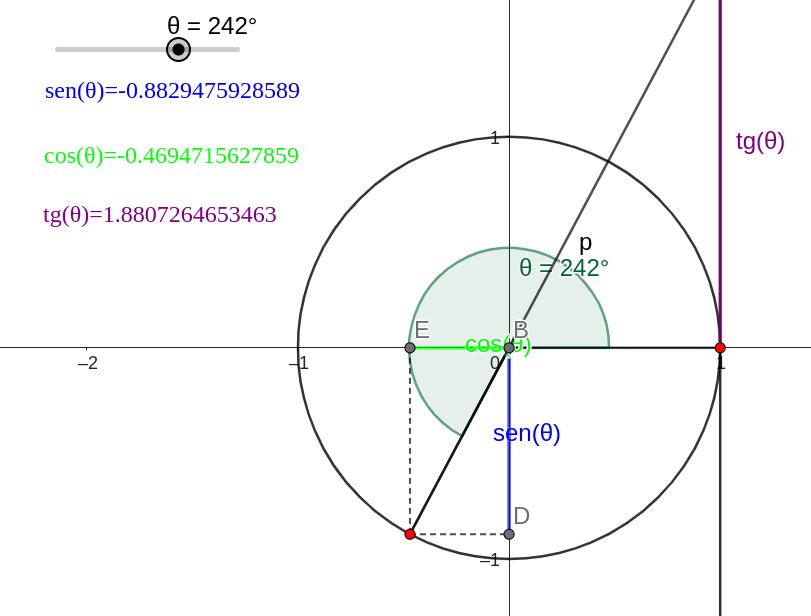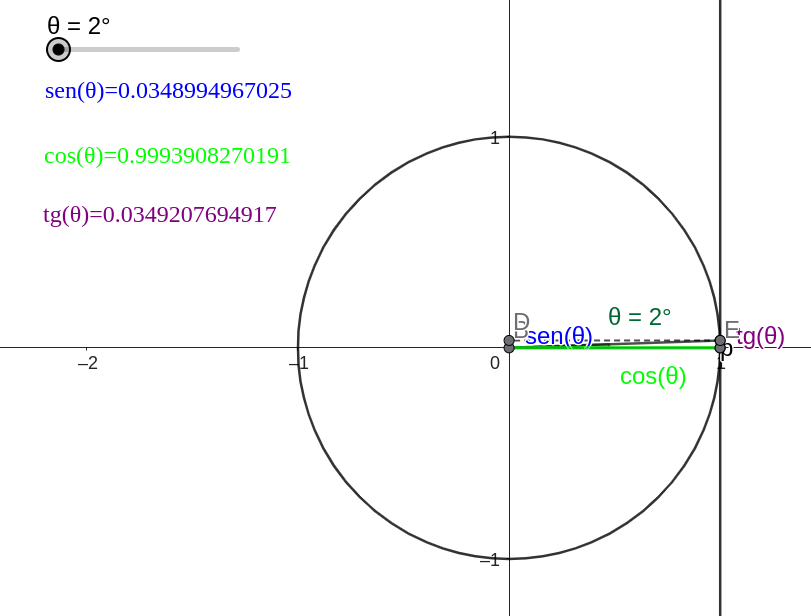
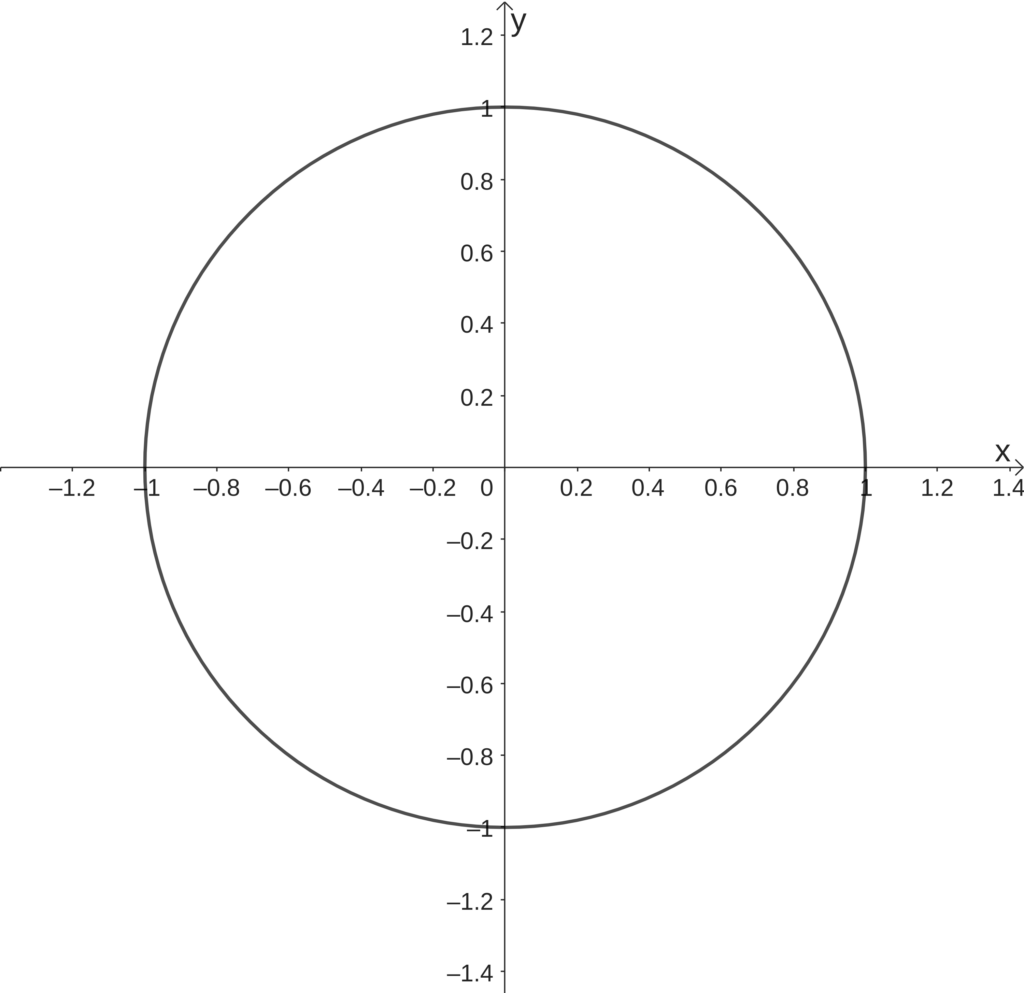
O círculo trigonométrico
é uma circunferência desenhada no plano cartesiano com centro no ponto (0,0) e raio 1.
Como determinar uma arco de ângulo [math] \theta [/math] no círculo trigonométrico
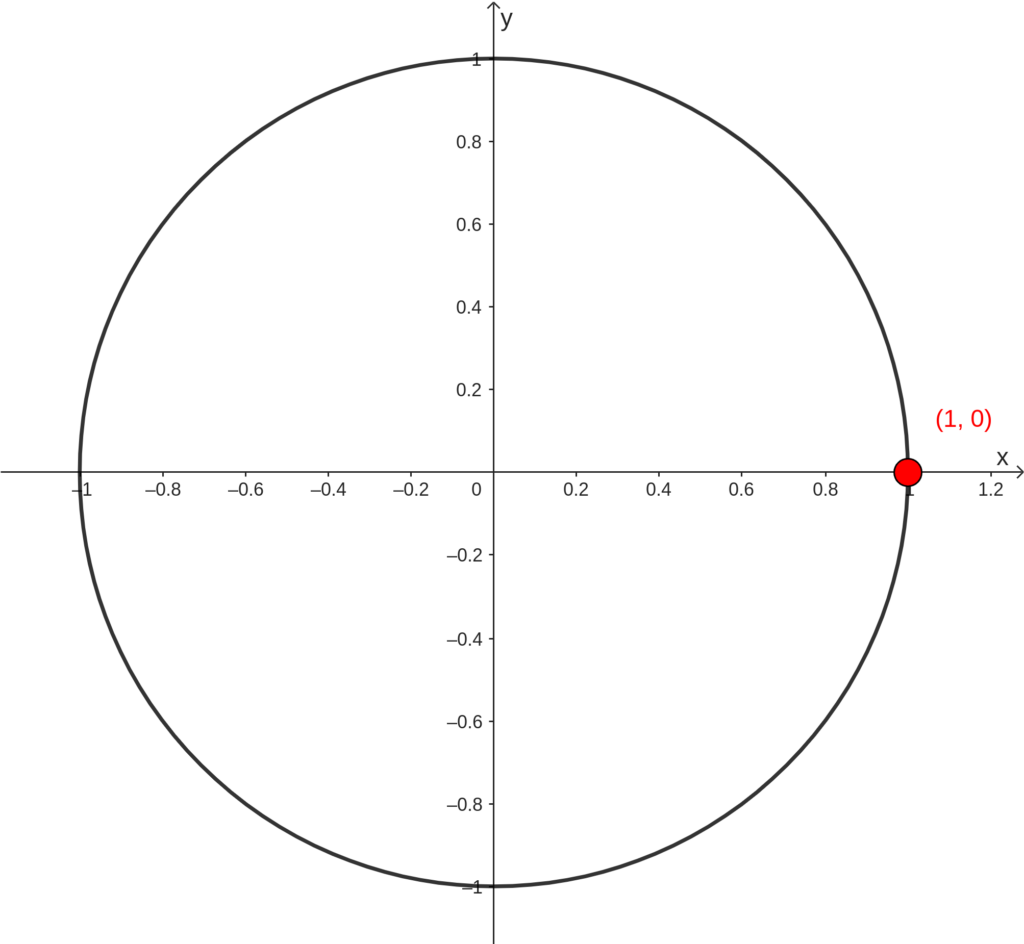
Levante o arco a partir do ponto (1,0), veja o ponto vermelho na figura:
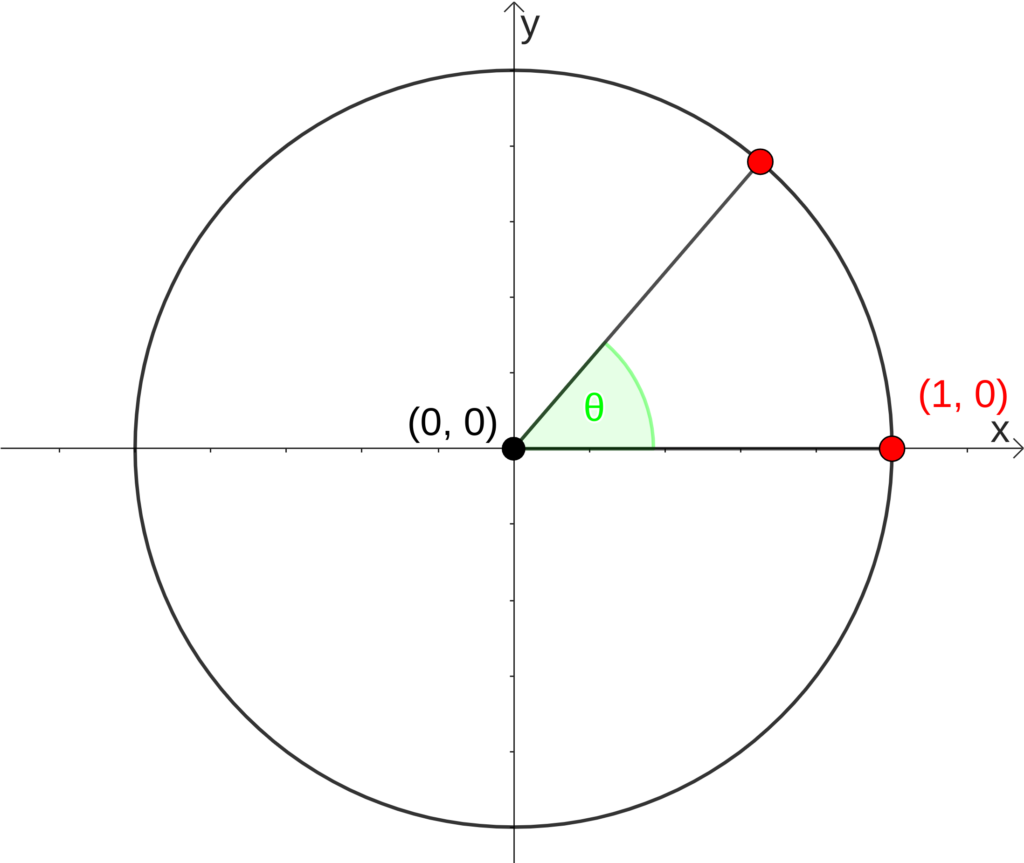
Agora é só levantar um arco, no sentido anti-horário, formando um ângulo de [math] \theta [/math] no ponto (0,0), como na figura:
Para definir o cosseno do ângulo [math] \theta [/math] vamos traçar um segmento a partir do ponto C em direção ao eixo X, como na figura:
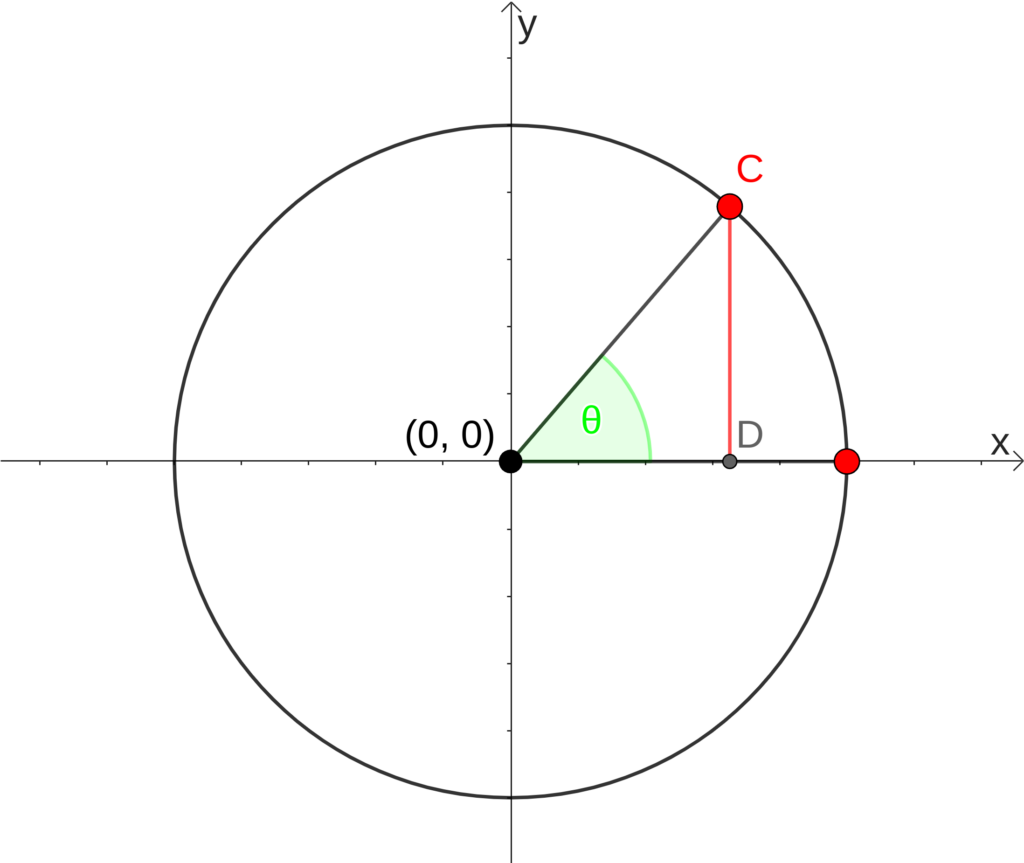
O cosseno do ângulo [math] \theta [/math] é determinado pela primeira coordenada do ponto D, ou seja, a distância entre o ponto (0,0) e o ponto D, que está em azul na figura abaixo:
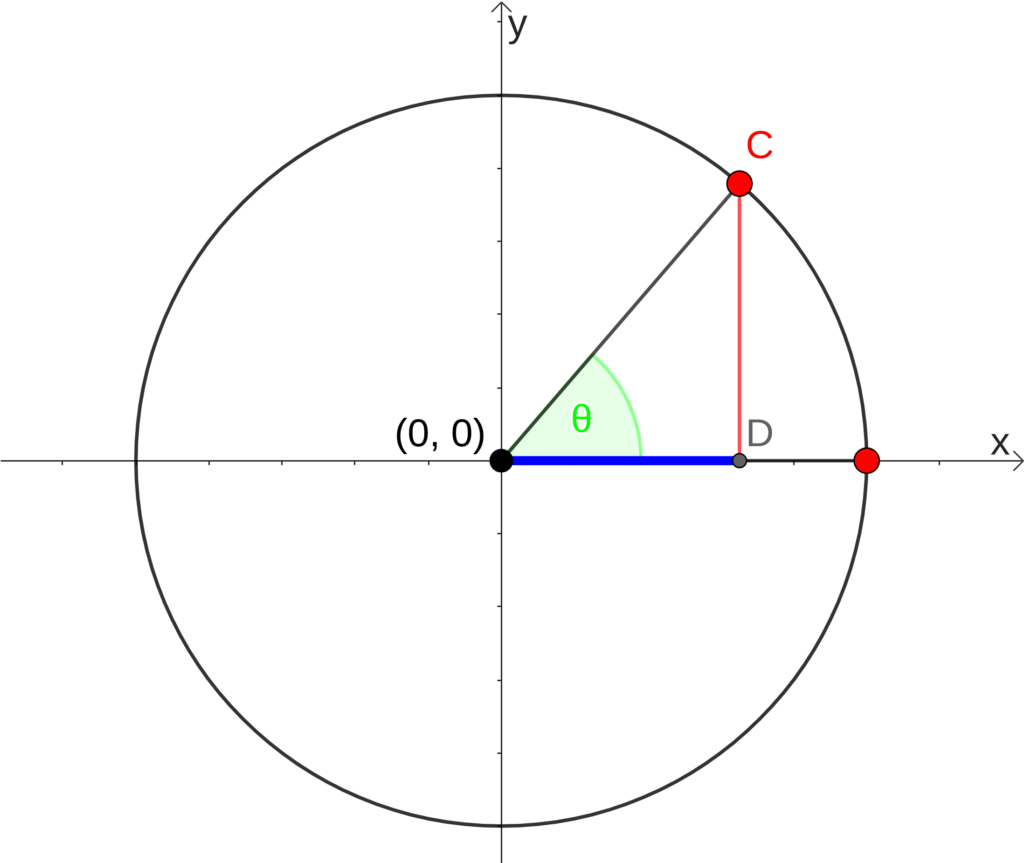
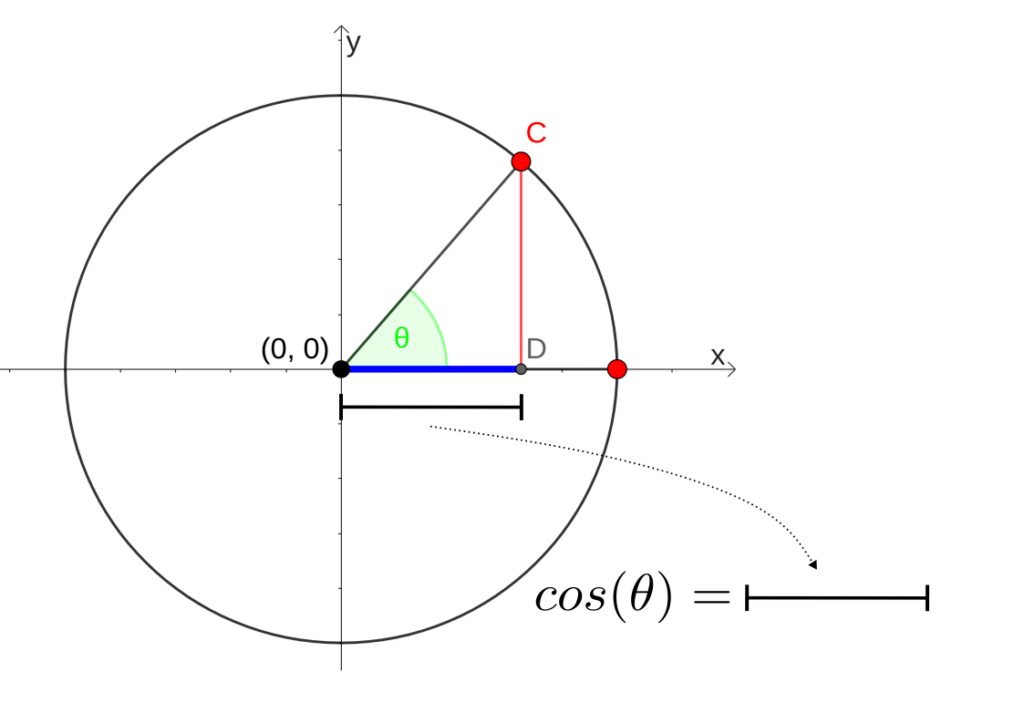
E denotamos o valor do cosseno de [math] \theta [/math] por [math] cos(\theta) [/math]
Por exemplo, o [math]cos(60^{\circ})=\frac{1}{2}[/math].
Veja na figura ao lado como o seguimento que representa o cosseno de 60 graus em azul
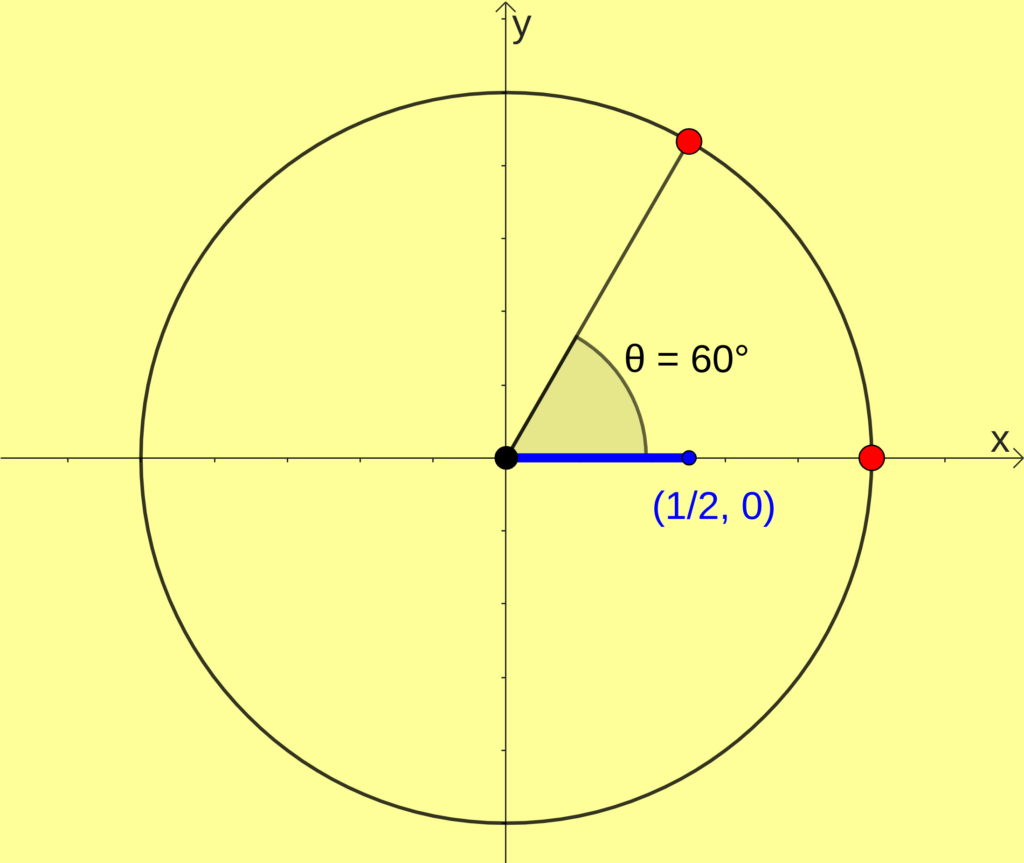
Podemos ter valores negativos para [math]cos(\theta)[/math]
Veja os exemplos:
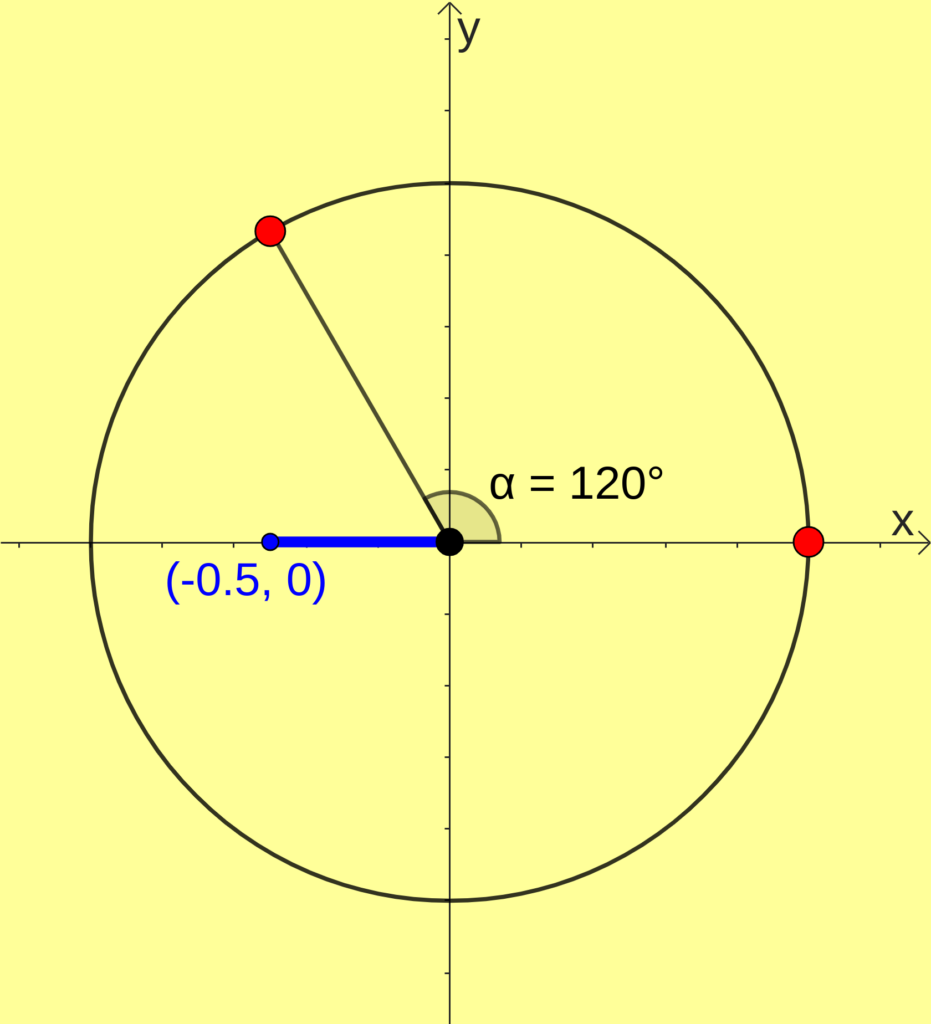
[math]cos(120^{\circ})=-\frac{1}{2}[/math]
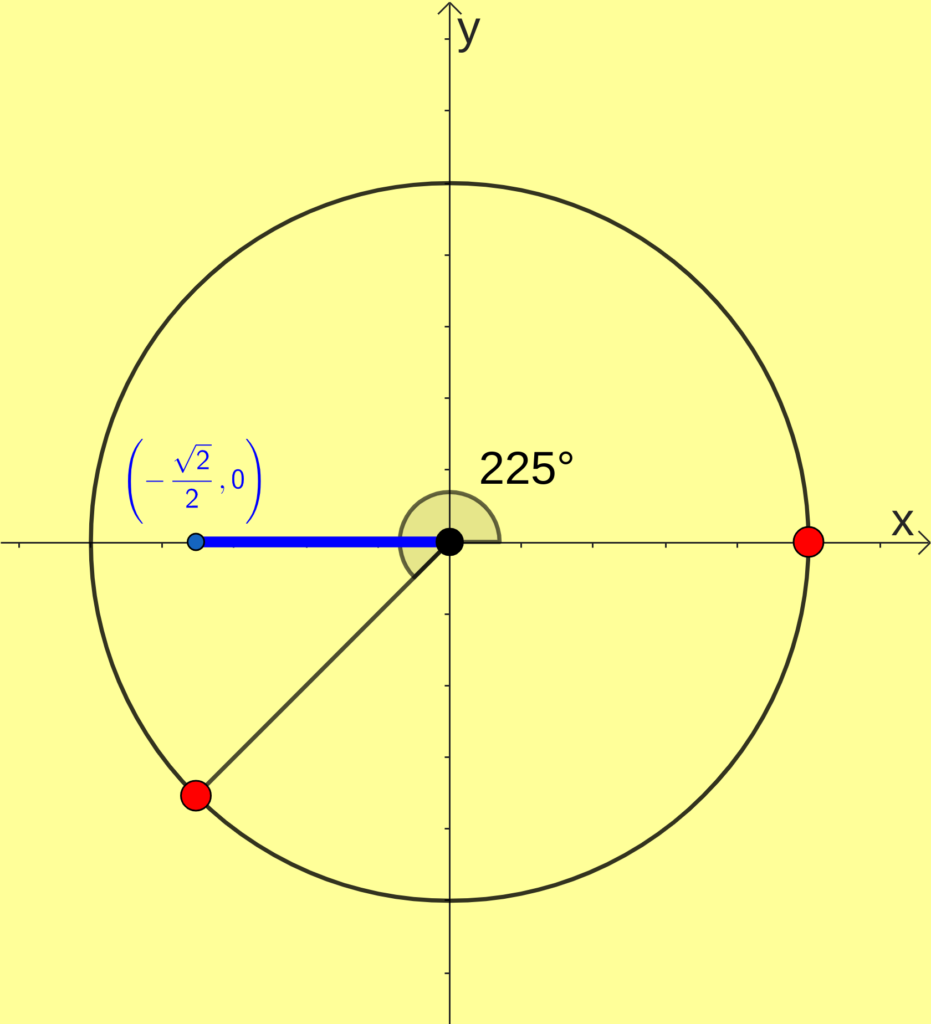
[math]cos(225^{\circ})=-\frac{\sqrt{2}}{2}[/math]
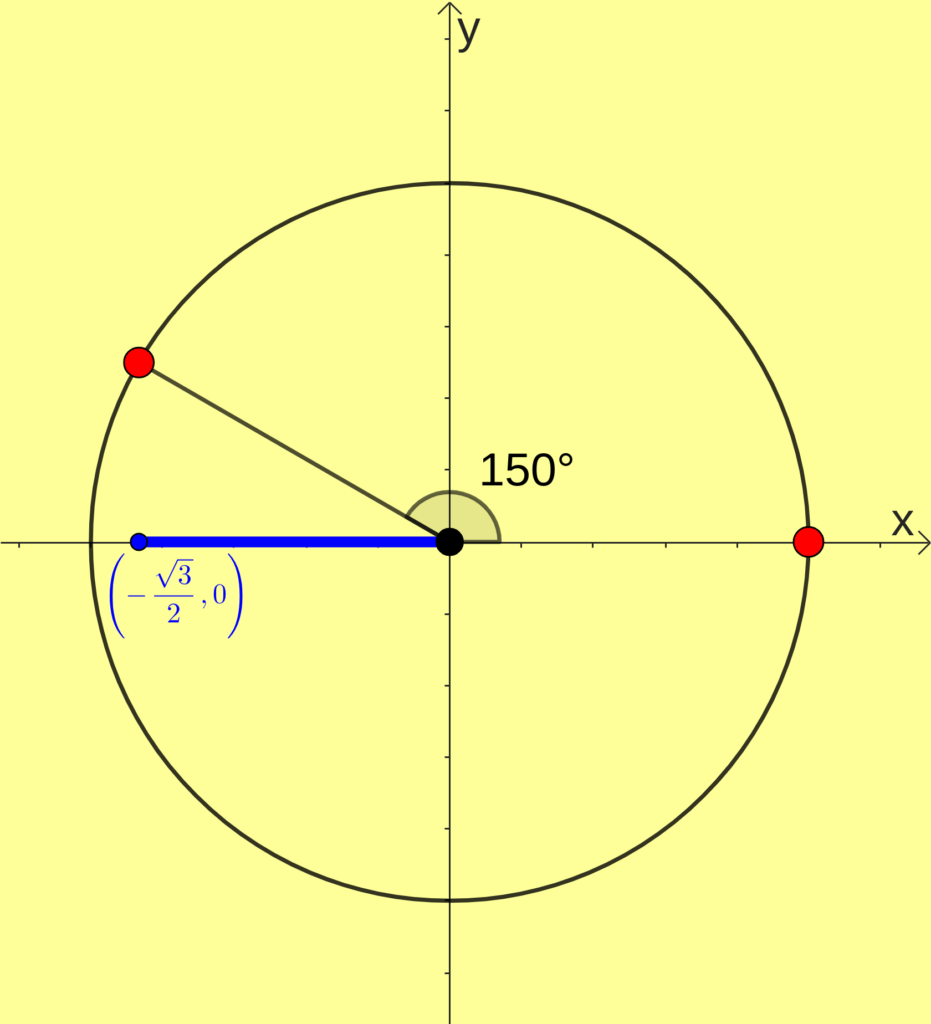
[math]cos(150^{\circ})=-\frac{\sqrt{3}}{2}[/math]
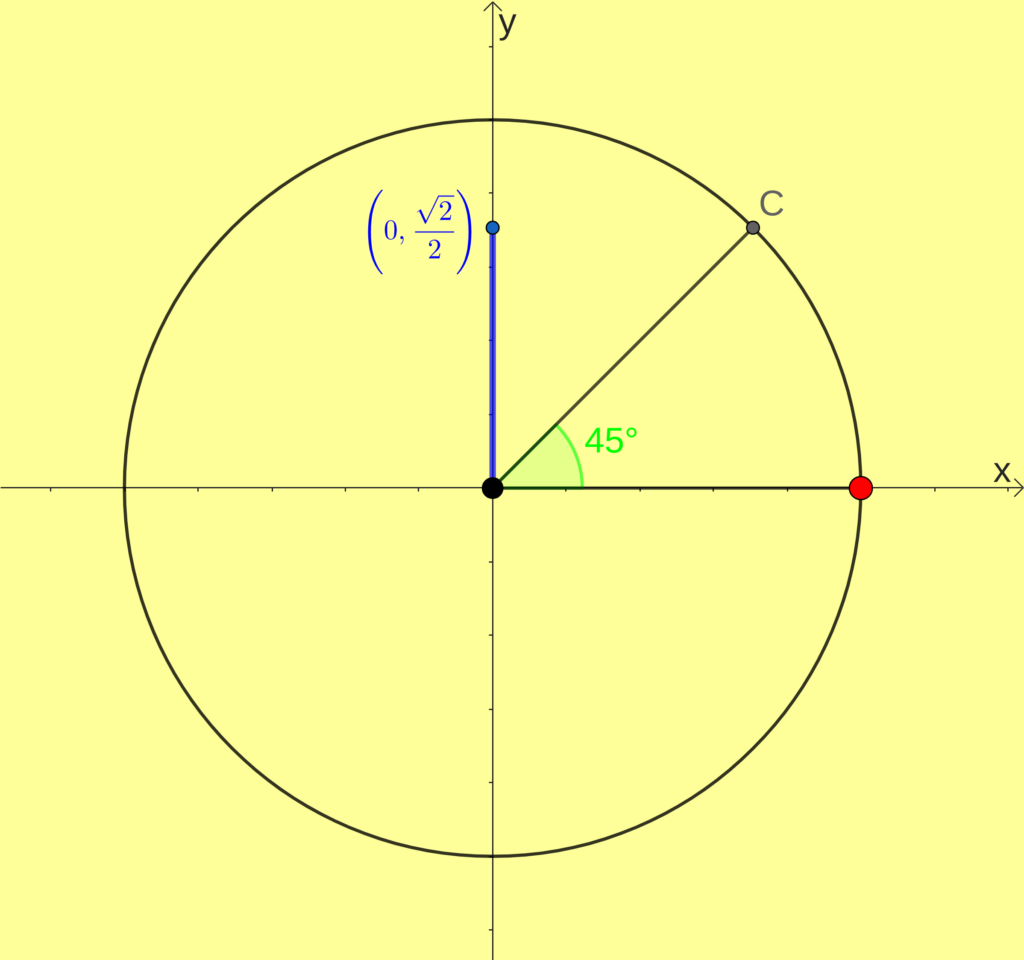
Para o seno de um ângulo [math]\theta[/math] vamos traçar um seguimento do ponto C em direção ao eixo y, como na figura
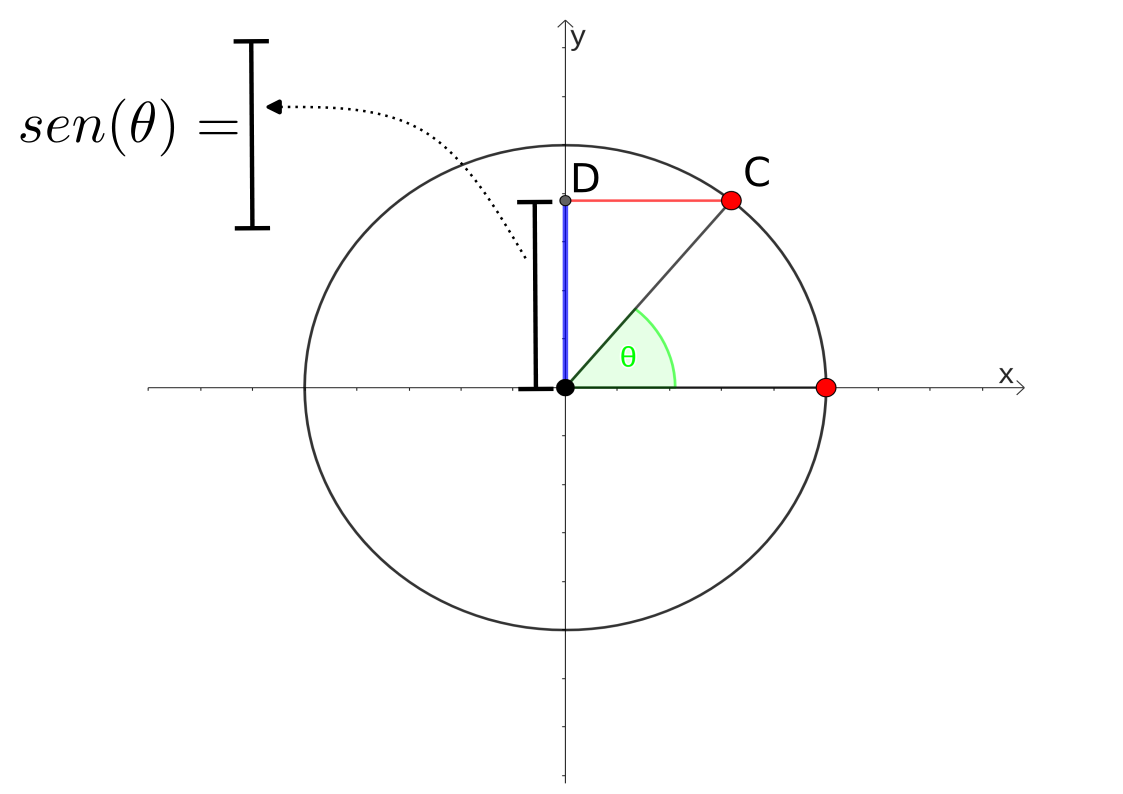
Ou seja, o seno do ângulo [math]\theta[/math] ([math]sen(\theta)[/math]) é determinado pela segunda coordenada do ponto D. Veja os exemplos:
[math]sen(45^{\circ})=\frac{\sqrt{2}}{2}[/math]
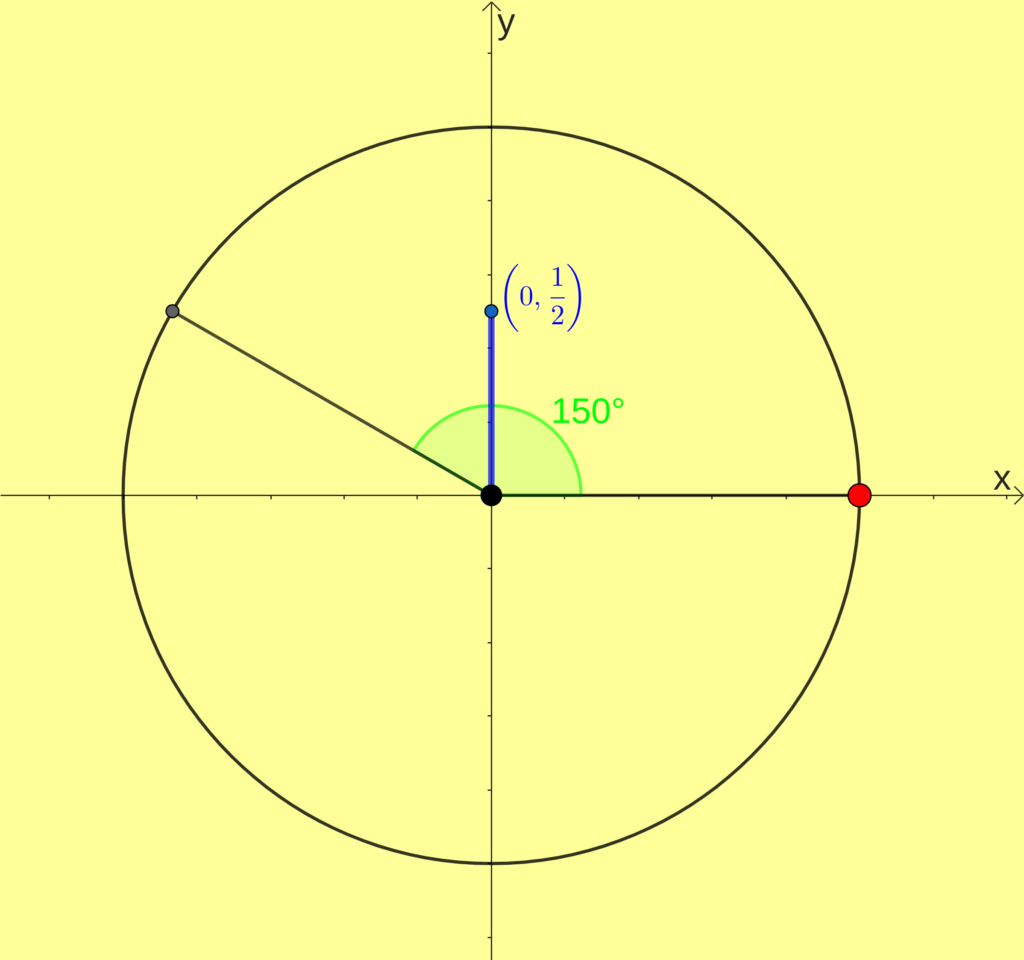
[math]sen(150^{\circ})=\frac{1}{2}[/math]
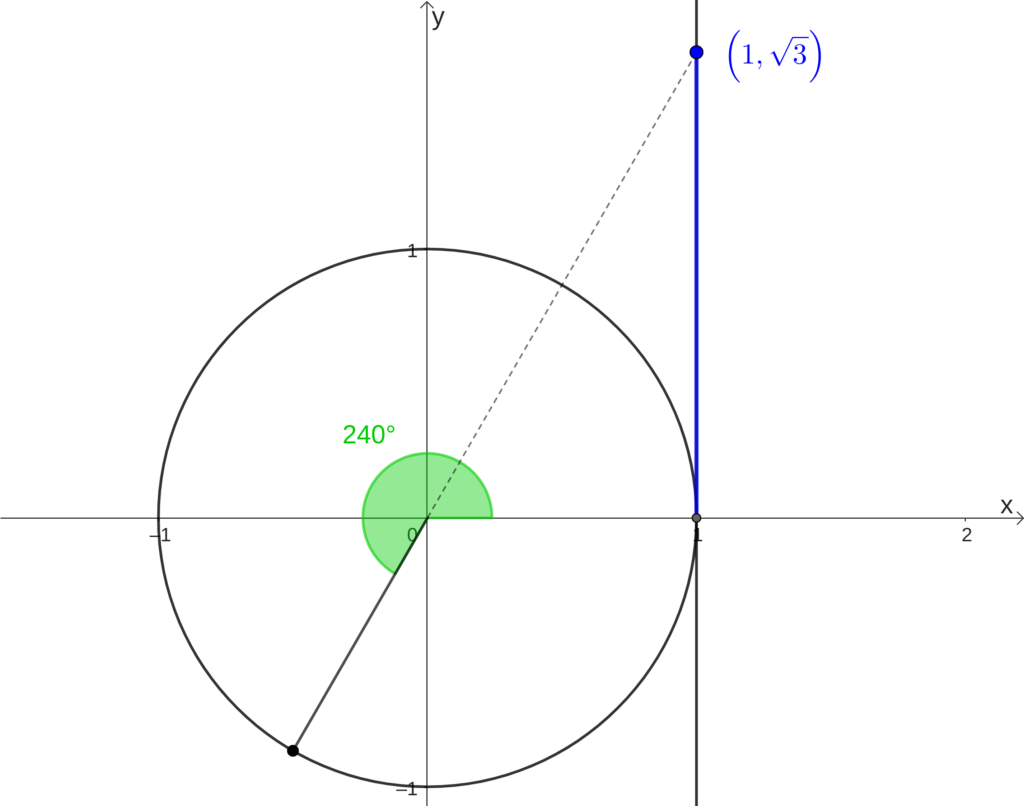
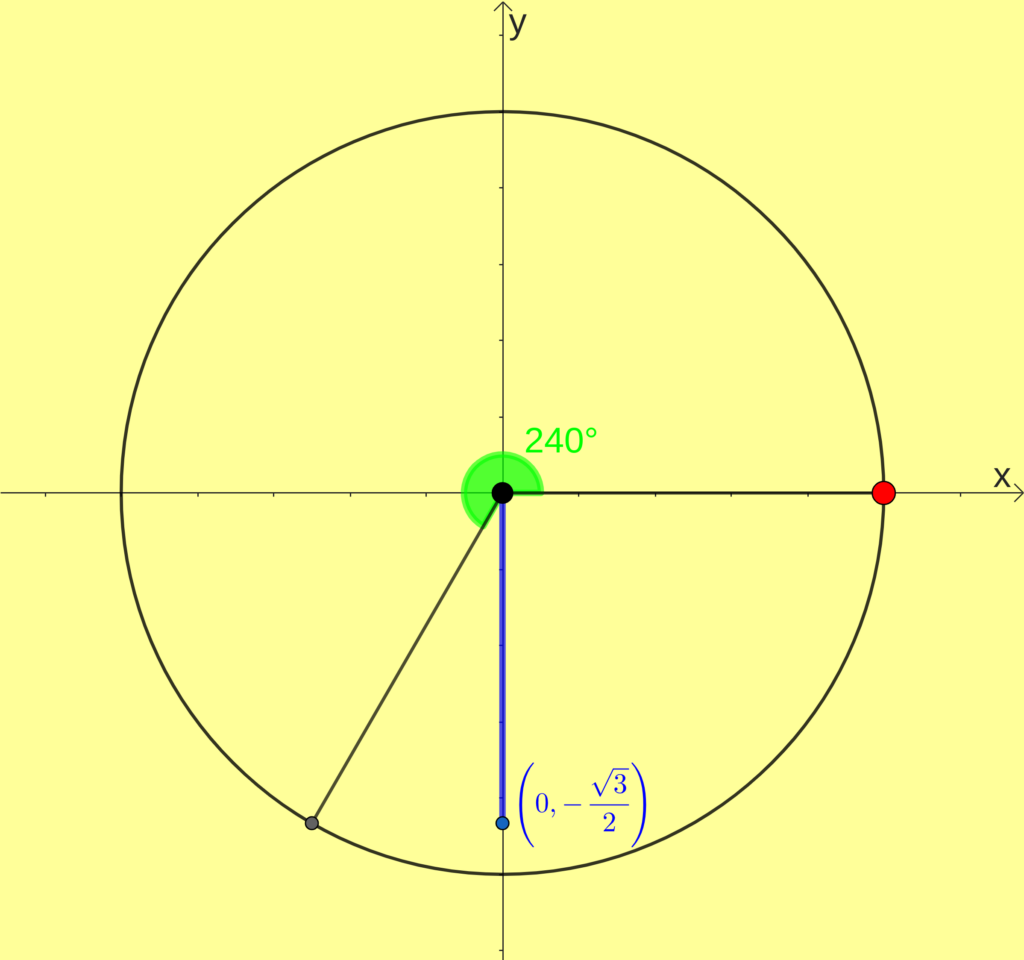
[math]sen(240^{\circ})=-\frac{\sqrt{3}}{2}[/math]
Para falar da tangente de um ângulo vamos precisar traçar uma reta auxiliar passando pelo ponto (1,0) no circulo trigonométrico e perpendicular ao eixo X, veja na figura
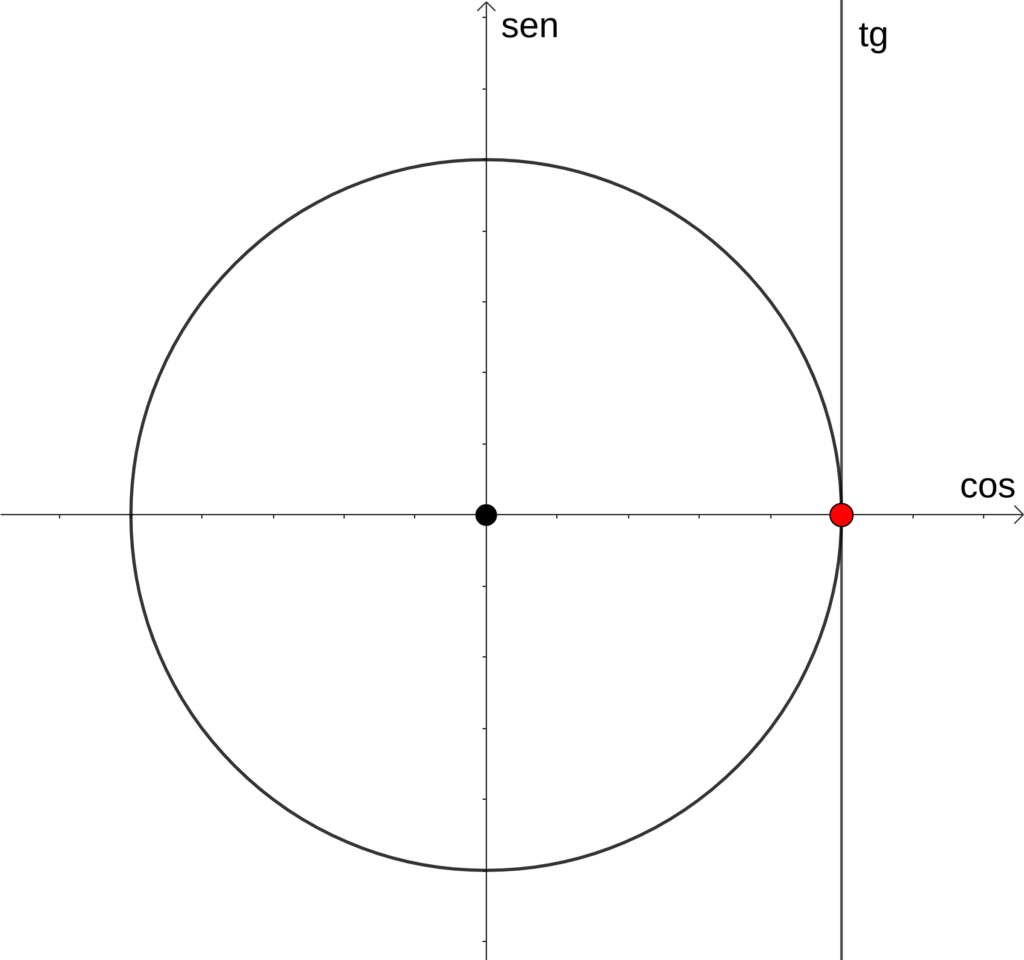
É comum denominarmos o eixo X de eixo dos cossenos e o eixo Y de eixo dos senos, essa nova reta auxiliar vamos denominar de eixo das tangentes. Como na figura
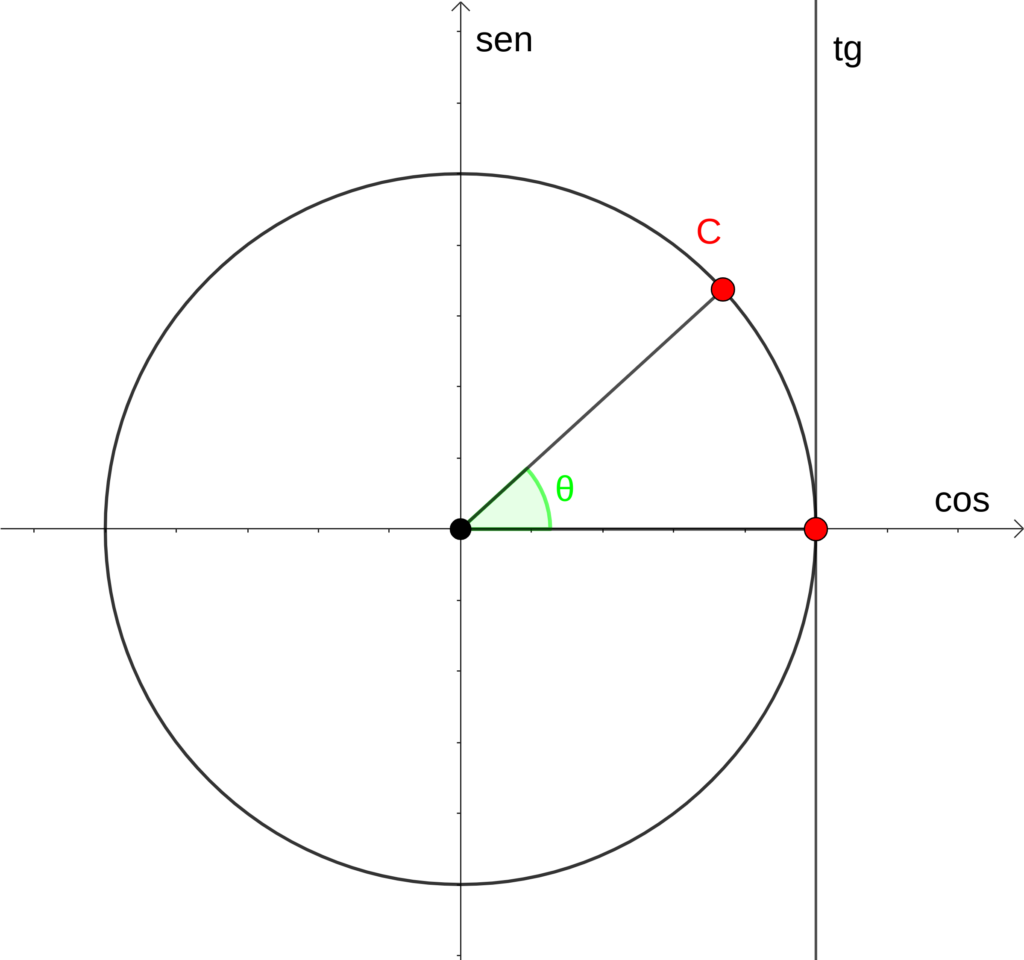
para determinar [math]tg(\theta)[/math] vamos estender o seguimento que sai do ponto (0,0) e passa pelo ponto C até encontrar o eixo da tangente
marcamos tal ponto com a letra D na próxima imagem

a tangente de [math]\theta[/math] é determinada pela segunda coordenada do ponto D
Ou seja, a tangente de um ângulo [math]\theta[/math] ([math]tg(\theta)[/math]) é determinada pela segunda coordenada do ponto D. Veja alguns exemplos:
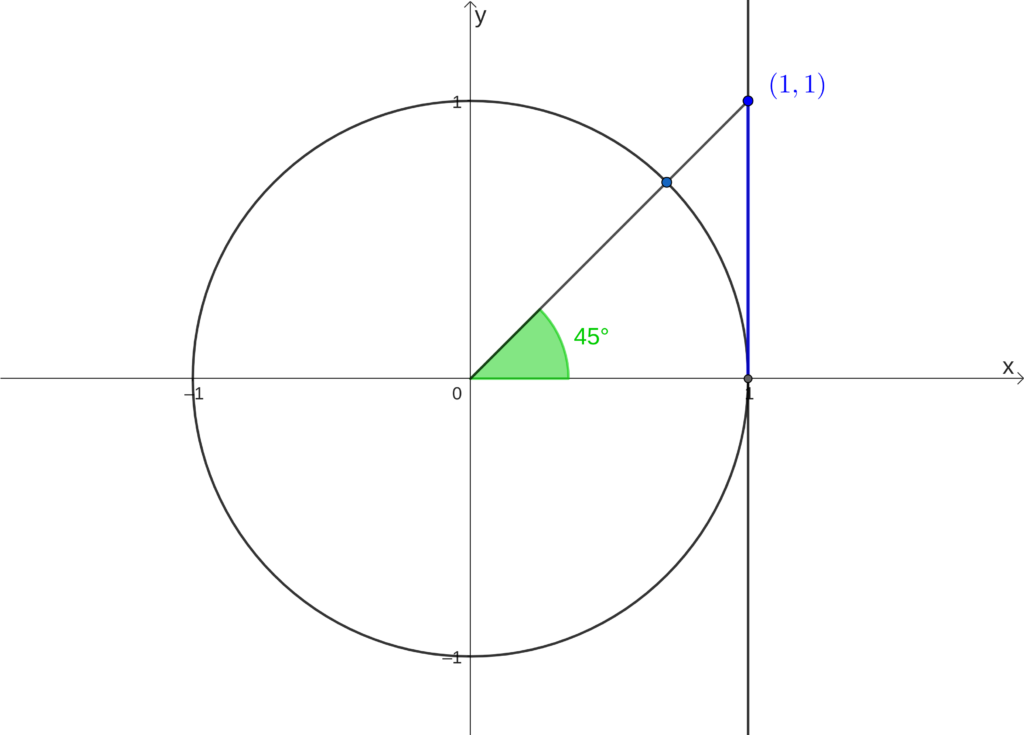
[math]tg(45^{\circ})=1[/math]
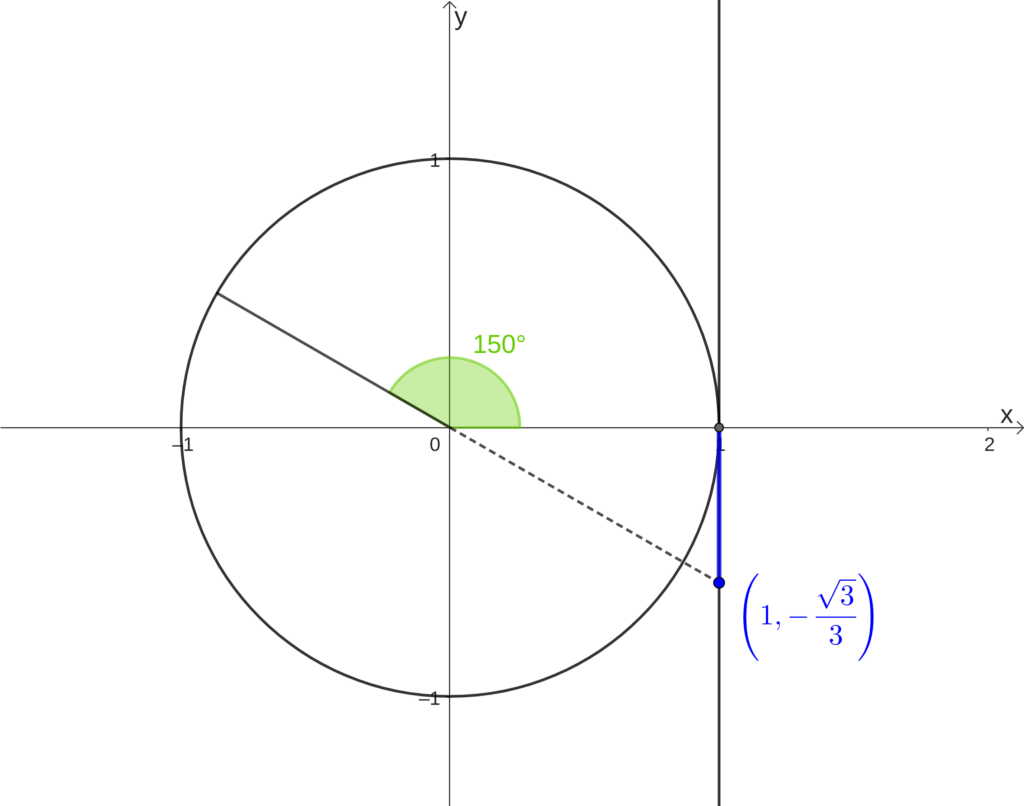
[math]tg(150^{\circ})=-\frac{\sqrt{3}}{3}[/math]
[math]tg(240^{\circ})=\sqrt{3}[/math]