Triângulos: Tipos, Propriedades e Curiosidades

Os triângulos são figuras geométricas formadas por três lados, três ângulos e três vértices. Apesar de parecerem simples, eles estão por toda parte – na arquitetura, nas pontes, nas placas de trânsito e até nas estruturas de aviões. Entender os triângulos é essencial para o estudo da Geometria Plana e para várias áreas da Matemática e Engenharia.

O que é um triângulo?

Um triângulo é o menor polígono que existe. Ele possui três lados, onde e a soma dos comprimentos de dois lados sempre é maior que o comprimento do terceiro lado. Essa é a famosa condição de existência de um triângulo. Para existir um triângulo com lados a, b e c, é preciso que:

a < b + c , b < a + c , c < a + b

Classificação dos triângulos

Os triângulos podem ser classificados pelo comprimento dos lados ou pela medida dos ângulos.

Quanto aos lados:

• Equilátero: três lados iguais e três ângulos iguais (60° cada). Exemplo: triângulo perfeito, muito usado em construções e logotipos;
• Isósceles: dois lados iguais e dois ângulos iguais. Exemplo: o telhado de uma casa ou uma placa de “dê a preferência”;
• Escaleno: todos os lados e ângulos diferentes. Exemplo: forma de um terreno irregular.

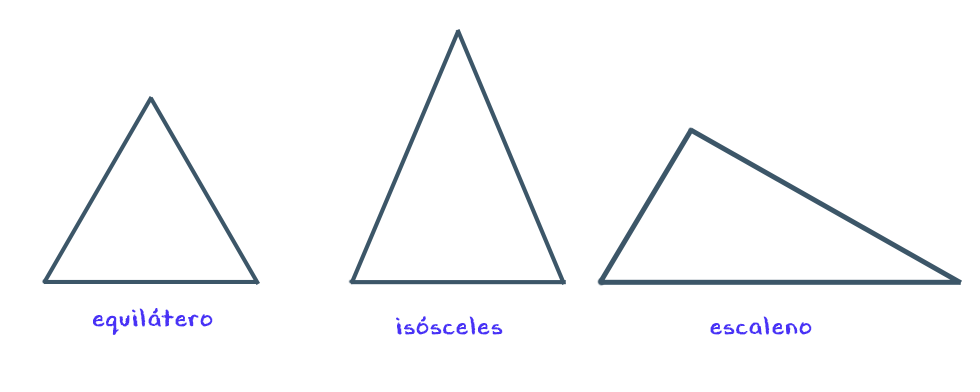
Fonte: Google, 2025.

Quanto aos ângulos:

• Acutângulo: todos os ângulos menores que 90°;
• Retângulo: tem um ângulo reto (90°), sendo o lado oposto ao ângulo reto, chamado de hipotenusa;
• Obtusângulo: tem um ângulo maior que 90°.

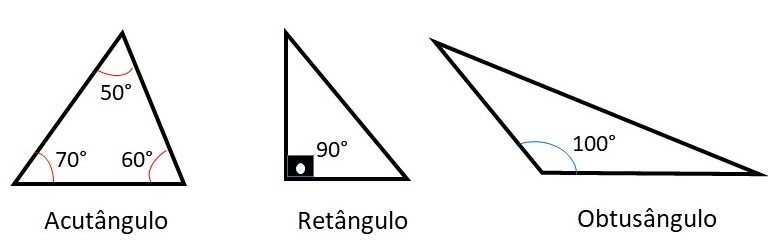Fonte: Google, 2025.

Elementos de um triângulo

• Lados: segmentos que formam o contorno;
• Vértices: pontos onde os lados se encontram;
• Ângulos internos: formados dentro do triângulo;
• Altura: segmento perpendicular traçado de um vértice até o lado oposto;
• Mediatriz, bissetriz e mediana: segmentos especiais que ajudam a estudar propriedades e construções geométricas;

Soma dos ângulos internos

A soma dos ângulos internos de qualquer triângulo é sempre 180°. Por exemplo, se dois ângulos medem 70° e 60°, o terceiro ângulo será 50°.

Área e Perímetro do triângulo

→ Perímetro (P): É a soma dos três lados

P = a + b + c

→ Área (A): Depende das informações conhecidas:

• Quando se conhece a base e a altura:

A = (base . altura) / 2

• Quando se conhecem os três lados (Fórmula de Herão):

A = √[p . (p – a) . (p – b) . (p – c)], onde p = (a + b + c) / 2 (semiperímetro)

O triângulo retângulo e o Teorema de Pitágoras

O triângulo retângulo é um dos mais importantes. Ele obedece ao Teorema de Pitágoras, que diz:

a² = b² + c², onde a é a hipotenusa, e b e c são os catetos

Esse teorema é a base para inúmeros cálculos de distância, altura e engenharia.

Exercício – Classificação de triângulos

Os lados de um triângulo medem 5 cm, 7 cm e 9 cm.
a) Verifique se é possível formar um triângulo.
b) Classifique-o quanto aos lados e quanto aos ângulos.

Resolução:

a) Condição de existência:
A soma de dois lados deve ser maior que o terceiro:
5 + 7 > 9 → 12 > 9 ✔️
5 + 9 > 7 → 14 > 7 ✔️
7 + 9 > 5 → 16 > 5 ✔️
É possível formar um triângulo.

b) Classificação pelos lados:
Os três lados têm medidas diferentes → Triângulo escaleno.

Classificação pelos ângulos:
Usa-se o teorema de Pitágoras para verificar:
9² = 81
5² + 7² = 25 + 49 = 74

Como 81 > 74, o maior lado ao quadrado é maior que a soma dos quadrados dos outros → Triângulo obtusângulo.

Resposta final: Triângulo escaleno e obtusângulo.

Curiosidades

• Todo triângulo pode ser inscrito em uma circunferência;
• A forma triangular é a mais estável e resistente das estruturas, por isso é usada em pontes e torres.