Volume de Sólidos Geométricos

O volume de um sólido geométrico representa a quantidade de espaço que ele ocupa no espaço tridimensional. Ele é expresso em unidades cúbicas, como  [math] \textbf{cm³}[/math], [math] \textbf{m³}[/math], entre outras. A seguir estão listadas algumas figuras geométricas mais comuns e suas respectivas equações para o cálculo do volume.

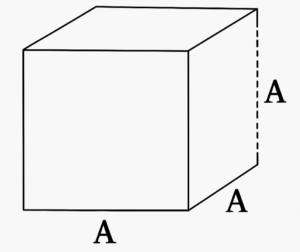
• Cubo
  
  O cubo é um sólido cujas faces são todas quadradas. Para calcular seu volume, usamos a fórmula:
  \[
  V = A^3
  \]
  Onde:
  \[
  “A”\ corresponde\ à\ medida\ da\ aresta.
  \]

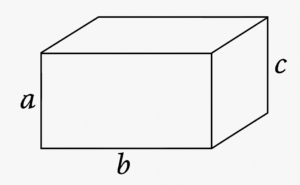
• Paralelepípedo
  
  O paralelepípedo possui seis faces retangulares. Sua equação para cálculo de volume é:
  \[
  V = a \times b \times c
  \]
  Onde:
  \[
  “a”,\ “b”\ e\ “c” são\ as\ medidas\ dos\ lados\ do\ paralelepípedo.
  \]

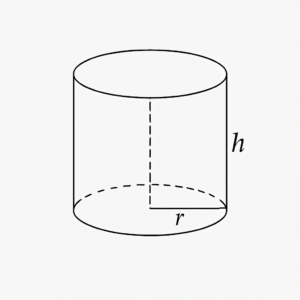
• Cilindro
  
  O cilindro tem bases circulares e altura perpendicular a essas bases. Seu volume é calculado por:
  \[ V = \pi r^2 h \]
  Onde:
  \[ “r”\ corresponde\ ao\ raio\ da\ base;\]
  \[“h”\ corresponde\ à\ altura\ do\ cilindro;\]
  \[“\pi”\  é\ aproximadamente\ 3,1416.\]

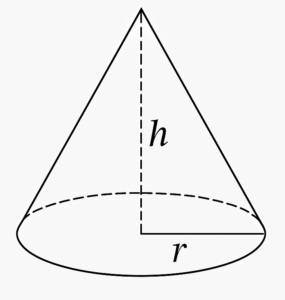
• Cone
  
  O cone possui uma base circular e uma altura que liga essa base ao vértice superior. A fórmula para seu volume é:
  \[ V = \frac{1}{3} \pi r^2 h \]
  Onde:
  \[ “r”\ corresponde\ ao\ raio\ da\ base;\]
  \[ “h”\ corresponde\ à\ altura\ do\ cone;\]
  \[“\pi”\  é\ aproximadamente\ 3,1416.\]

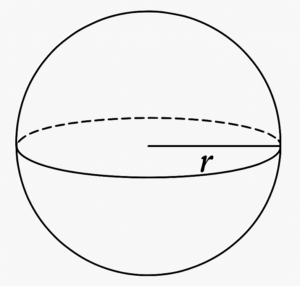
• Esfera
  
  A esfera é um sólido perfeitamente redondo. Seu volume é dado por:
  \[ V = \frac{4}{3} \pi r^3 \]
  Onde:
  \[“r” \ corresponde\ ao\ raio\ da\ esfera.\]

• Pirâmide
  
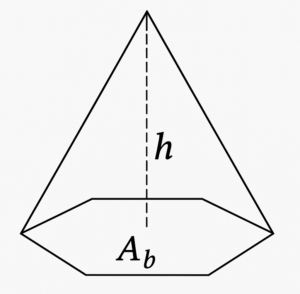
  A pirâmide tem uma base poligonal e faces laterais triangulares que se encontram em um vértice comum. O volume é calculado por:
  \[ V = \frac{1}{3} A_b h \]
  Onde:
  \[“A_b”\ corresponde\ a\ área\ da\ base;\]
  \[“h”\ corresponde\ à\ altura\ da\ pirâmide.\]

Exercício-(Enem 2016) Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m³. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.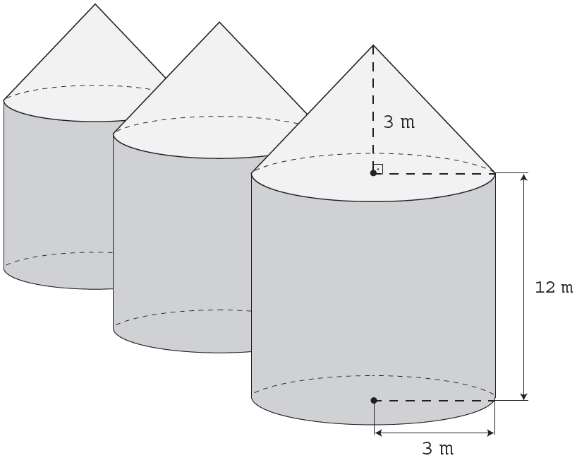

Utilize 3 como aproximação para π.

O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é

A) 6.

B) 16.

C) 17.

D) 18.

E) 21.

• Resolução

Inicialmente, calcularemos o volume de um silo, que é composto por um cilindro e um cone.

O volume do cilindro é dado por:

\begin{equation}
V_{\text{cilindro}} = \pi r^2 h
\end{equation}

Substituindo os valores dados:

\begin{equation}
V_{\text{cilindro}} = \pi \times 3^2 \times 12
\end{equation}

\begin{equation}
V_{\text{cilindro}} = \pi \times 9 \times 12
\end{equation}

\begin{equation}
V_{\text{cilindro}} = 108\pi
\end{equation}

Agora, calculamos o volume do cone, com raio de 3 m e altura de 3 m:

\begin{equation}
V_{\text{cone}} = \frac{1}{3} \pi r^2 h
\end{equation}

\begin{equation}
V_{\text{cone}} = \frac{1}{3} \pi \times 3^2 \times 3
\end{equation}

\begin{equation}
V_{\text{cone}} = \frac{1}{3} \pi \times 9 \times 3
\end{equation}

\begin{equation}
V_{\text{cone}} = \frac{27}{3} \pi = 9\pi
\end{equation}

Utilizando π = 3 e somando os volumes do cilindro e do cone, temos:

\begin{equation}
V_{\text{silo}} = 9 \times 3 + 108 \times 3
\end{equation}

\begin{equation}
V_{\text{silo}} = 27 + 324 = 351 \text{ m}^3
\end{equation}

O caminhão leva 20 m³ por viagem, então o número de viagens necessárias é:

\begin{equation}
\frac{351}{20} = 17,55
\end{equation}

Serão necessárias, portanto, 18 viagens.
Alternativa D